在直角三角形从 $ABC$ 中，$\angle C$ 是直角，$CA=30$，$CB=16$ 。三角形外两点 ${{O}_{1}}$，${{O}_{2}}$ 分别是两个相切的等圆的圆心。以 ${{O}_{1}}$ 为圆心的圆与三角形斜边及直角边 $CA$ 的延长线（越过 $A$ 的方向）相切，以 ${{O}_{2}}$ 为圆心的圆与三角形斜边及直角 $CB$ 的延长线（越过 $B$ 的方向）相切，这两个圆的半径可以表示为 $\frac{p}{q}$，其中 $p$，$q$ 是互素的正整数，求 $p+q$ 。
【难度】
【出处】
2007年第25届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
737
【解析】
如图25-2所示，令 ${{T}_{1}}$ 和 ${{T}_{2}}$ 分别是两圆在 $AB$ 上的切点，则 ${{O}_{1}}{{T}_{1}}$ 和 ${{O}_{2}}{{T}_{2}}$ 都是半径，长度均为 $r$ 。设两圆相切于点 ${{T}_{3}}$，圆 $O_{1}^{{}}$ 切 $\overline{CA}$ 延长线于点 ${{E}_{1}}$，圆 ${{O}_{2}}$ 切 $\overline{CB}$ 延长线于点 ${{E}_{2}}$，设直线 ${{O}_{1}}{{O}_{2}}$ 与直线 $CA$、$CB$ 分别交于点 ${{p}_{1}}$，${{p}_{2}}$，直线 ${{O}_{1}}{{E}_{1}}$ 与直线 ${{O}_{2}}{{E}_{2}}$ 相交于点 $D$ 。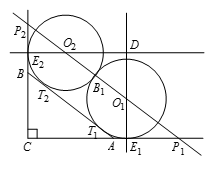
由 ${{O}_{1}}{{T}_{1}}\bot{{T}_{1}}{{T}_{2}}$，${{O}_{2}}{{T}_{2}}\bot {{T}_{1}}{{T}_{2}}$ 及 ${{O}_{1}}{{T}_{1}}\bot{{O}_{2}}{{T}_{2}}$ 知四边形 ${{O}_{1}}{{O}_{2}}{{T}_{2}}{{T}_{1}}$ 是矩形，故 ${{O}_{1}}{{O}_{2}}\parallel{{T}_{2}}{{T}_{1}}$，因此三角形 ${{O}_{1}}{{O}_{2}}D$ 和 $BAC$ 的三边分别平行，故它们相似。由 ${{O}_{1}}{{O}_{2}}={{O}_{1}}{{T}_{3}}+{{O}_{2}}{{T}_{3}}=2r$ 知 ${{O}_{1}}D=2r\cdot\frac{16}{34}=\frac{16}{17}r$，${{O}_{2}}D=2r\cdot\frac{30}{34}=\frac{30}{17}r$ 。因此 ${{E}_{1}}D=\frac{16}{17}r+r=\frac{33}{17}r$，${{E}_{2}}D=\frac{30}{17}r+r=\frac{47}{17}r$，故在矩形 $C{{E}_{1}}D{{E}_{2}}$ 中，$C{{E}_{2}}=\frac{33}{17}r$，$C{{E}_{1}}=\frac{47}{17}r$ 。
由于三角形 ${{P}_{1}}{{E}_{1}}{{O}_{1}}$ 与 $ACB$ 的三边分别平行，故它们相似，因此 ${{P}_{1}}{{E}_{1}}=r\cdot\frac{30}{16}=\frac{15}{8}r$，故 $C{{P}_{1}}={{P}_{1}}{{E}_{1}}+C{{E}_{1}}=\frac{15}{8}r+\frac{47}{17}r=\frac{631}{136}r$，再根据三角形 ${{P}_{1}}C{{P}_{2}}$ 与 $ACB$ 相似 $C{{P}_{2}}=\frac{631}{136}r\cdot\frac{16}{30}=\frac{631}{255}r$，${{P}_{1}}{{P}_{2}}=\frac{631}{136}r\cdot\frac{34}{30}=\frac{631}{120}r$，故由面积法得到斜边 ${{P}_{1}}{{P}_{2}}$ 上的高为 $\frac{\frac{631}{255}r\cdot\frac{631}{136}r}{\frac{631}{120}r}=\frac{631}{289}r$ 。故点 $C$ 到 $AB$ 的距离为 $\frac{631}{289}r-r=\frac{342}{289}r$，但另一方面，由面积法知点 $C$ 到 $AB$ 的距离为 $\frac{16\cdot30}{34}=\frac{240}{17}$，故 $\frac{342}{289}r=\frac{240}{17}$，解得 $r=\frac{680}{57}$，因此所求的值为 $\frac{680}{57}=737$ 。
由 ${{O}_{1}}{{T}_{1}}\bot{{T}_{1}}{{T}_{2}}$，${{O}_{2}}{{T}_{2}}\bot {{T}_{1}}{{T}_{2}}$ 及 ${{O}_{1}}{{T}_{1}}\bot{{O}_{2}}{{T}_{2}}$ 知四边形 ${{O}_{1}}{{O}_{2}}{{T}_{2}}{{T}_{1}}$ 是矩形，故 ${{O}_{1}}{{O}_{2}}\parallel{{T}_{2}}{{T}_{1}}$，因此三角形 ${{O}_{1}}{{O}_{2}}D$ 和 $BAC$ 的三边分别平行，故它们相似。由 ${{O}_{1}}{{O}_{2}}={{O}_{1}}{{T}_{3}}+{{O}_{2}}{{T}_{3}}=2r$ 知 ${{O}_{1}}D=2r\cdot\frac{16}{34}=\frac{16}{17}r$，${{O}_{2}}D=2r\cdot\frac{30}{34}=\frac{30}{17}r$ 。因此 ${{E}_{1}}D=\frac{16}{17}r+r=\frac{33}{17}r$，${{E}_{2}}D=\frac{30}{17}r+r=\frac{47}{17}r$，故在矩形 $C{{E}_{1}}D{{E}_{2}}$ 中，$C{{E}_{2}}=\frac{33}{17}r$，$C{{E}_{1}}=\frac{47}{17}r$ 。由于三角形 ${{P}_{1}}{{E}_{1}}{{O}_{1}}$ 与 $ACB$ 的三边分别平行，故它们相似，因此 ${{P}_{1}}{{E}_{1}}=r\cdot\frac{30}{16}=\frac{15}{8}r$，故 $C{{P}_{1}}={{P}_{1}}{{E}_{1}}+C{{E}_{1}}=\frac{15}{8}r+\frac{47}{17}r=\frac{631}{136}r$，再根据三角形 ${{P}_{1}}C{{P}_{2}}$ 与 $ACB$ 相似 $C{{P}_{2}}=\frac{631}{136}r\cdot\frac{16}{30}=\frac{631}{255}r$，${{P}_{1}}{{P}_{2}}=\frac{631}{136}r\cdot\frac{34}{30}=\frac{631}{120}r$，故由面积法得到斜边 ${{P}_{1}}{{P}_{2}}$ 上的高为 $\frac{\frac{631}{255}r\cdot\frac{631}{136}r}{\frac{631}{120}r}=\frac{631}{289}r$ 。故点 $C$ 到 $AB$ 的距离为 $\frac{631}{289}r-r=\frac{342}{289}r$，但另一方面，由面积法知点 $C$ 到 $AB$ 的距离为 $\frac{16\cdot30}{34}=\frac{240}{17}$，故 $\frac{342}{289}r=\frac{240}{17}$，解得 $r=\frac{680}{57}$，因此所求的值为 $\frac{680}{57}=737$ 。
答案
解析
备注
