设 $ABC$ 是一个等边三角形,$D$ 和 $F$ 分别是 $BC$ 和 $AB$ 上的点,并满足以 $FA=5$ 及 $CD=2$,点 $E$ 在边 $CA$ 以上,且满足 $\angle DEF={{60}^{\circ }}$ 。已知三角形 $DEF$ 的面积为 $14\sqrt{3}$ 。若边 $AB$ 长的两个可能值为 $p\pm q\sqrt{r}$,其中 $p$,$q$ 是有理数,$r$ 是一个不被任何素数的平方整除的整数。求 $r$ 。
【难度】
【出处】
2007年第25届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
989
【解析】
如图25-4所示,设 $AE=k$,$CE=l$,由 $\angle CED={{180}^{\circ}}-{{60}^{\circ }}-\angle AEF=\angle EAF$ 及 $\angle A=\angle C={{60}^{\circ }}$ 得 $\vartriangle AEF\sim \vartriangle CDE$,故 $\frac{5}{k}=\frac{l}{2}$,即 $kl=10$ 。由余弦定理得 $EF=\sqrt{{{k}^{2}}-5k+25}$,$DE=\sqrt{{{l}^{2}}-2l+4}$,再由正弦定理得 $14\sqrt{3}=\frac{1}{2}DE\cdot EF\cdot \sin {{60}^{\circ }}$,故 $DE\cdot EF=56$ 。将前面两式代入得 $\sqrt{{{k}^{2}}-5k+25}\cdot\sqrt{{{l}^{2}}-2l+4}=56$,将 $l=\frac{10}{k}$ 代入整理得 $\frac{2}{k}\left({{k}^{2}}-5k+25 \right)=56$,解得 $k=\frac{33\pm \sqrt{989}}{2}$,因此
$AB=k+l=k+\frac{10}{k}=\frac{231}{10}\pm\frac{3}{10}\sqrt{989}$ 。
经检验两个 $k$ 值所导出的图形均满足题目条件,故所求的 $r$ 为 $989$ 。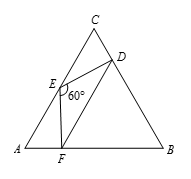
$AB=k+l=k+\frac{10}{k}=\frac{231}{10}\pm\frac{3}{10}\sqrt{989}$ 。
经检验两个 $k$ 值所导出的图形均满足题目条件,故所求的 $r$ 为 $989$ 。

答案
解析
备注