两根长圆柱管平行摆放在平面上，这两根圆柱管长度相同，但底面直径不同，大圆柱管底面半径为 $72$，沿平面向小圆柱管的方向滚动，小圆柱管底面半径为 $24$，大圆柱管滚过小圆柱管并贴在小圆柱管表面继续向前滚动，最后停止运动时，大圆柱管停在与出发时圆周同一点处，并完成了自身的一周转动。若小圆柱管自身不滚动（也不移动），大圆柱管滚动过程中不发生滑动，那么大圆柱管的起点和终点相距 $x$ 。 $x$ 可表示为 $a\pi +b\sqrt{c}$ 的形式，其中 $a$，$b$，$c$ 整数，$c$ 不能被任何素数的平方整除。试求 $a+b+c$ 。
【难度】
【出处】
2007年第25届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
179
【解析】
如图25-7所示，设大圆柱管滚动到与小圆柱管相切时停止滚动。在那一点处，两柱体底面的水平圆心距为 $d$，其中 $d$ 为直角三角形的一条直角边，斜边和另一条直角边长度分别为 $72+24=96$，$72-24=48$，即这个直角三角形的三角分别为 ${{30}^{\circ }}$，${{60}^{\circ }}$，${{90}^{\circ }}$，其中 ${{30}^{\circ }}$ 是小圆柱管底面的圆心角，$d=48\sqrt{3}$，大圆柱管停止滚动所处的点与跟小圆柱管相切的点的夹角为 ${{60}^{\circ }}$ 。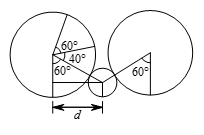
当大圆柱管经过小圆柱管，它与小圆柱管的另一边相切，它的圆心移动的水平距离为 $2d=96\sqrt{3}$ 。滚动小圆柱管 ${{180}^{\circ }}-2\left({{30}^{\circ }} \right)={{120}^{\circ }}$ 的弧长，因此它滚动大圆柱管上 ${{120}^{\circ }}$ 所对弧长的三分之一即 ${{40}^{\circ }}$ 所对的弧长。大圆柱管从经过小圆柱管之前停留的点到经过小圆柱管停留的点间转动 ${{60}^{\circ }}+{{40}^{\circ}}+{{60}^{\circ }}={{160}^{\circ }}$ 。因此大圆柱管滚了 ${{160}^{\circ }}$ 所对的弧长，移动的水平距离为 $96\sqrt{3}$ 。当大圆柱管完成一周转动，共滚了 ${{360}^{\circ}}-{{160}^{\circ }}={{200}^{\circ }}$ 所对的弧长，移动的水平距离为 $96\sqrt{3}$ 。因此，总共的水平距离为 $\frac{200}{360}\cdot 72\cdot2\pi +96\sqrt{3}=80\pi +96\sqrt{3}$ 。即 $a+b+c=80+96+3=179$ 。
当大圆柱管经过小圆柱管，它与小圆柱管的另一边相切，它的圆心移动的水平距离为 $2d=96\sqrt{3}$ 。滚动小圆柱管 ${{180}^{\circ }}-2\left({{30}^{\circ }} \right)={{120}^{\circ }}$ 的弧长，因此它滚动大圆柱管上 ${{120}^{\circ }}$ 所对弧长的三分之一即 ${{40}^{\circ }}$ 所对的弧长。大圆柱管从经过小圆柱管之前停留的点到经过小圆柱管停留的点间转动 ${{60}^{\circ }}+{{40}^{\circ}}+{{60}^{\circ }}={{160}^{\circ }}$ 。因此大圆柱管滚了 ${{160}^{\circ }}$ 所对的弧长，移动的水平距离为 $96\sqrt{3}$ 。当大圆柱管完成一周转动，共滚了 ${{360}^{\circ}}-{{160}^{\circ }}={{200}^{\circ }}$ 所对的弧长，移动的水平距离为 $96\sqrt{3}$ 。因此，总共的水平距离为 $\frac{200}{360}\cdot 72\cdot2\pi +96\sqrt{3}=80\pi +96\sqrt{3}$ 。即 $a+b+c=80+96+3=179$ 。
答案
解析
备注
