三角形数表中的第一行数字按照奇数1,3,5,…,99的递增顺序书写,在第一行下面的每一行比上一行少一个数字,最底部的一行只有一个数字.每行的相邻两个数字之和写在这两个数字中间的下一行的位置.这个数表中有多少个数是67的倍数?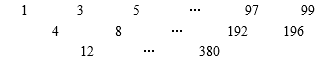
【难度】
【出处】
2008年第26届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
17
【解析】
在三角阵列中,第 $r$ 行是一个以 ${{2}^{r}}$ 为公差的等差数列,由归纳法可证第 $r$ 行的第一个元素为 $r\cdot{{2}^{r-1}}$,因此第 $r$ 行的第 $n$ 个元素为
$r\cdot{{2}^{2-1}}+\left( n-1 \right){{2}^{r}}={{2}^{r-1}}\left( r+2n-2 \right)$;$1\leqslant n\leqslant 51-r$.
若 ${{2}^{r-1}}\left(r+2n-2 \right)$ 为67的倍数,则 $r+2n-2$ —定为67的倍数,由 $1\leqslant n\leqslant 51-r$ 得
$1\leqslant r\leqslant r+2n-2\leqslant r+2\left( 51-r \right)-2=100-r\leqslant 99$.
故只有 $r+2n-2=67$,即 $r$ 为奇数,且 $r\leqslant67\leqslant 100-r$.因此 $r$ 必须是1到33之间的奇数,这样的 $r$ 有17个,每个 $r$ 对应一个满足条件的 $n$,故67的倍数共有17个.
$r\cdot{{2}^{2-1}}+\left( n-1 \right){{2}^{r}}={{2}^{r-1}}\left( r+2n-2 \right)$;$1\leqslant n\leqslant 51-r$.
若 ${{2}^{r-1}}\left(r+2n-2 \right)$ 为67的倍数,则 $r+2n-2$ —定为67的倍数,由 $1\leqslant n\leqslant 51-r$ 得
$1\leqslant r\leqslant r+2n-2\leqslant r+2\left( 51-r \right)-2=100-r\leqslant 99$.
故只有 $r+2n-2=67$,即 $r$ 为奇数,且 $r\leqslant67\leqslant 100-r$.因此 $r$ 必须是1到33之间的奇数,这样的 $r$ 有17个,每个 $r$ 对应一个满足条件的 $n$,故67的倍数共有17个.
答案
解析
备注