图26-3所示是一个 $4\times 4$ 的点阵,最近的两个点相距为1个单位,定义一个生长路径是点阵中不同点之间的一个序列,且连续两点之间的距离严格单调(这个点列中第1、2个点间距离小于第2、3个点间距离,第2、3个点间距离于第3、4个点间距离……).一条生长路径所含点数目的最大值为 $m$,恰好含有 $m$ 个点的生长路径一共有 $r$ 条,求 $m\cdot r$ 的值.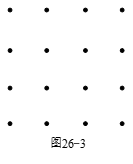

【难度】
【出处】
2008年第26届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
240
【解析】
我们来证明 $m=10$ 和 $r=24$.注意到在这个 $4\times 4$ 的点阵中(图26-5),任何两点的距离形如 $\sqrt{{{a}^{2}}+{{b}^{2}}}$,$a$,$b\in \left\{ 0 ,1 ,2, 3 \right\}$.不同的距离有9种,分别为 $\sqrt{1}$,$\sqrt{2}$,$\sqrt{4}$,$\sqrt{5}$,$\sqrt{8}$,$\sqrt{9}$,$\sqrt{10}$,$\sqrt{13}$ 和 $\sqrt{18}$.因此一条生长路线上最多含有10个点.对于一条生长路线,不妨设其上的10个点依次为 ${{p}_{1}}$,${{p}_{2}}$,…,${{p}_{10}}$.如图26-5所示,首先可知 ${{p}_{9}}{{p}_{10}}=\sqrt{18}$,即 ${{p}_{9}}$ 和 ${{p}_{10}}$ 分别位于这个点阵对角线的两端点,${{p}_{9}}$ 和 ${{p}_{10}}$ 在这个点阵中一共有4种排列.${{p}_{8}}$ 在 ${{p}_{10}}$ 的旁边两个对称的位置之一.注意到右上角不可能是 ${{p}_{7}}$,否则有 ${{p}_{6}}={{p}_{9}}$ 或 ${{p}_{6}}={{p}_{10}}$.容易发现 ${{p}_{7}}$,${{p}_{6}}$,${{p}_{5}}$,${{p}_{4}}$,${{p}_{3}}$ 和 ${{p}_{2}}$ 都是固定的,最后只有 ${{p}_{1}}$ 有三种可能的位置,即 $r=4\cdot2\cdot 3=24$,所以 $mr=240$ 为所求.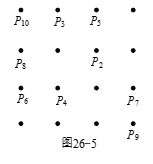

答案
解析
备注