在 $\vartriangle ABC$ 中，$AB=AC=100$，$BC=56$．⊙ $P$ 的半径为16，且与边 $AC$，$BC$ 相切．⊙ $Q$ 位于 $\vartriangle ABC$ 内部，且与⊙ $P$，$AB$，$BC$ 都相切．⊙ $Q$ 的半径可以写成 $m-n\sqrt{k}$ 的形式，其中 $m$，$n$，$k$ 都是正整数，且 $k$ 为一些不同素数之积，求 $m+nk$ 的值．
【难度】
【出处】
2008年第26届美国数学邀请赛Ⅱ（AIMEⅡ）
【标注】
【答案】
254
【解析】
如图26-6所示，不妨设⊙ $Q$ 的半径为 $q$，边 $BC$ 分别切⊙ $P$，⊙ $Q$ 于点 $M$，$N$．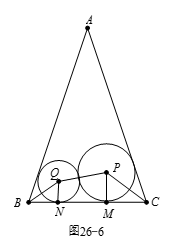
易知 $\cos\angle ABC=\frac{28}{100}=\frac{7}{25}$，由 $BQ$ 平分 $ABC$ 及二倍角公式得 $1-2{{\sin}^{2}}\angle QBC=\frac{7}{25}$，结合 $\angle QBC$ 是锐角可得 $\sin\angle QBC=\frac{3}{5}$．同理 $\sin\angle PCB=\frac{3}{5}$．
因引 $\cot\angle QBC=\cot \angle PCB=\frac{4}{3}$，故 $BN=\frac{4}{3}q$，$CM=\frac{4}{3}\cdot 16$．故 $MN=BC-BN-CM=\frac{104-4q}{3}$．
另一方面，两个外切的圆的外公切线长应等于它们半径的几何平均值的2倍（这可以使用勾股定理来证明），故 $MN=2\sqrt{16q}$．因此 $2\sqrt{16q}=\frac{104-4q}{3}$．
两边平方，展开并去分母得 ${{q}^{2}}-88q+676=0$，故 $q=44\pm 6\sqrt{35}$．注意到 $MN=\frac{104-4q}{3}0$，故 $q26$，因此 $q=44+6\sqrt{35}$ 应舍去，故 $q=44-6\sqrt{35}$，所求的 $m+nk=44+6\cdot35=254$．
易知 $\cos\angle ABC=\frac{28}{100}=\frac{7}{25}$，由 $BQ$ 平分 $ABC$ 及二倍角公式得 $1-2{{\sin}^{2}}\angle QBC=\frac{7}{25}$，结合 $\angle QBC$ 是锐角可得 $\sin\angle QBC=\frac{3}{5}$．同理 $\sin\angle PCB=\frac{3}{5}$．因引 $\cot\angle QBC=\cot \angle PCB=\frac{4}{3}$，故 $BN=\frac{4}{3}q$，$CM=\frac{4}{3}\cdot 16$．故 $MN=BC-BN-CM=\frac{104-4q}{3}$．
另一方面，两个外切的圆的外公切线长应等于它们半径的几何平均值的2倍（这可以使用勾股定理来证明），故 $MN=2\sqrt{16q}$．因此 $2\sqrt{16q}=\frac{104-4q}{3}$．
两边平方，展开并去分母得 ${{q}^{2}}-88q+676=0$，故 $q=44\pm 6\sqrt{35}$．注意到 $MN=\frac{104-4q}{3}0$，故 $q26$，因此 $q=44+6\sqrt{35}$ 应舍去，故 $q=44-6\sqrt{35}$，所求的 $m+nk=44+6\cdot35=254$．
答案
解析
备注
