在 $\vartriangle ABC$ 中,$AC=450$,$BC=300$,点 $K$ 是边 $AC$ 的中点,$\angle ACB$ 的平分线交边 $AB$ 于点 $L$.设 $P$ 是 $BK$ 与 $CL$ 的交点,延长 $PK$ 到 $M$,使得 $KM=PK$.若 $AM=180$,求 $LP$ 的长度.
【难度】
【出处】
2009年第27届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
72
【解析】
如图所示,因四边形 $APCM$ 的对角线互相平分,故 $APCM$ 为平行四边形,于是 $AM$ 平行于 $CP$.又 $\vartriangle ABM\tilde{ }\vartriangle LBP$,故 $\frac{AM}{LP}=\frac{AB}{BL}=1+\frac{AL}{BL}$.由角平分线性质定理可知 $\frac{AL}{LB}=\frac{AC}{BC}$.因此 $\frac{AM}{LP}=1+\frac{AC}{BC}=\frac{AC+BC}{BC}$,故 $LP=\frac{AM\cdot BC}{AC+BC}=\frac{180\cdot 300}{450+300}=72$.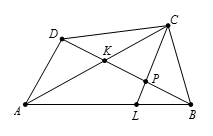

答案
解析
备注