在 $\vartriangle ABC$ 中,$AB=10$,$BC=14$,$CA=16$.$D$ 是线段 $BC$ 上一点,${{I}_{B}}$,${{I}_{C}}$ 分别是 $\vartriangle ABD$,$\vartriangle ACD$ 的内心.$\vartriangle B{{I}_{B}}D$,$\vartriangle C{{I}_{C}}D$ 的外接圆交于两不同点 $P$,$Q$.$\vartriangle BPC$ 的面积的最大值可以表示为 $a-b\sqrt{c}$ 的形式,其中 $a b c$ 都是正整数且 $c$ 不能被任何素数的平方整除.求 $a+b+c$.
【难度】
【出处】
2009年第27届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
150
【解析】
如图所示,注意到
$\angle B{{I}_{B}}D=\angle {{I}_{B}}BA+\angle BAD+\angle AD{{I}_{B}}=\angle BAD+\frac{\angle DBA}{2}+\frac{\angle ADB}{2}$
和
$\angle C{{I}_{C}}D=\angle {{I}_{C}}DA+\angle DAC+\angle AC{{I}_{C}}=\angle DAC+\frac{\angle CDA}{2}+\frac{\angle ACD}{2}$,
由 $\angle BAD+\angle DAC=\angle BAC$ 及 $\angle ADB+\angle CDA={{180}^{\circ }}$,故
$\angle B{{I}_{B}}D+\angle C{{I}_{C}}D=\angle BAC+\frac{\angle ACD}{2}+\frac{\angle DBA}{2}+{{90}^{\circ }}={{180}^{\circ}}+\frac{\angle BAC}{2}$.(27-1)
点 $P$ 和 ${{I}_{B}}$ 一定位于 $BC$ 的两侧,且 $B{{I}_{B}}DP$ 和 $C{{I}_{C}}DP$ 都是圆内接凸四边形.这是因为,若 $P$ 和 ${{I}_{B}}$ 位于 $BC$ 的同侧,则 $B{{I}_{B}}PD$ 和 $C{{I}_{C}}PD$ 都是圆内接凸四边形,由(27-1)可知
$\angle BPC=\angle BPD+\angle DPC=\angle B{{I}_{B}}D+\angle C{{I}_{C}}D={{180}^{\circ }}+\frac{\angle BAC}{2}{{180}^{\circ }}$,这是不可能的.
由(27-1)可知,
$\angle BPC=\angle BPD+\angle DPC+{{180}^{\circ}}-\angle B{{I}_{B}}D+{{180}^{\circ }}-\angle C{{I}_{C}}D={{180}^{\circ }}-\frac{\angle BAC}{2}$.
因此,$\angle BPC$ 是一个常数,故 $P$ 位于 $B$,$C$ 圆弧上.由余弦定理可知,$\cos \angle BAC=\frac{{{10}^{2}}+{{16}^{2}}-{{14}^{2}}}{2\cdot 10\cdot 16}=\frac{1}{2}$,故 $\angle BAC={{60}^{\circ }}$,于是 $\angle BPC={{150}^{\circ }}$,当 $BP=PC$ 时 $\vartriangle BPC$ 的面积取到最大值.设 $BP=PC=x$,对 $\vartriangle BPC$ 应用余弦定理得 ${{14}^{2}}=2{{x}^{2}}+{{x}^{2}}\sqrt{3}$,故 ${{x}^{2}}=\frac{196}{2+\sqrt{3}}=196\left(2-\sqrt{3} \right)$.于是,$\vartriangle BPC$ 的面积为 $\frac{1}{2}{{x}^{2}}\sin {{150}^{\circ}}=98-49\sqrt{3}$,故 $a+b+c=150$.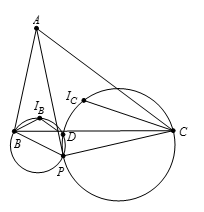
$\angle B{{I}_{B}}D=\angle {{I}_{B}}BA+\angle BAD+\angle AD{{I}_{B}}=\angle BAD+\frac{\angle DBA}{2}+\frac{\angle ADB}{2}$
和
$\angle C{{I}_{C}}D=\angle {{I}_{C}}DA+\angle DAC+\angle AC{{I}_{C}}=\angle DAC+\frac{\angle CDA}{2}+\frac{\angle ACD}{2}$,
由 $\angle BAD+\angle DAC=\angle BAC$ 及 $\angle ADB+\angle CDA={{180}^{\circ }}$,故
$\angle B{{I}_{B}}D+\angle C{{I}_{C}}D=\angle BAC+\frac{\angle ACD}{2}+\frac{\angle DBA}{2}+{{90}^{\circ }}={{180}^{\circ}}+\frac{\angle BAC}{2}$.(27-1)
点 $P$ 和 ${{I}_{B}}$ 一定位于 $BC$ 的两侧,且 $B{{I}_{B}}DP$ 和 $C{{I}_{C}}DP$ 都是圆内接凸四边形.这是因为,若 $P$ 和 ${{I}_{B}}$ 位于 $BC$ 的同侧,则 $B{{I}_{B}}PD$ 和 $C{{I}_{C}}PD$ 都是圆内接凸四边形,由(27-1)可知
$\angle BPC=\angle BPD+\angle DPC=\angle B{{I}_{B}}D+\angle C{{I}_{C}}D={{180}^{\circ }}+\frac{\angle BAC}{2}{{180}^{\circ }}$,这是不可能的.
由(27-1)可知,
$\angle BPC=\angle BPD+\angle DPC+{{180}^{\circ}}-\angle B{{I}_{B}}D+{{180}^{\circ }}-\angle C{{I}_{C}}D={{180}^{\circ }}-\frac{\angle BAC}{2}$.
因此,$\angle BPC$ 是一个常数,故 $P$ 位于 $B$,$C$ 圆弧上.由余弦定理可知,$\cos \angle BAC=\frac{{{10}^{2}}+{{16}^{2}}-{{14}^{2}}}{2\cdot 10\cdot 16}=\frac{1}{2}$,故 $\angle BAC={{60}^{\circ }}$,于是 $\angle BPC={{150}^{\circ }}$,当 $BP=PC$ 时 $\vartriangle BPC$ 的面积取到最大值.设 $BP=PC=x$,对 $\vartriangle BPC$ 应用余弦定理得 ${{14}^{2}}=2{{x}^{2}}+{{x}^{2}}\sqrt{3}$,故 ${{x}^{2}}=\frac{196}{2+\sqrt{3}}=196\left(2-\sqrt{3} \right)$.于是,$\vartriangle BPC$ 的面积为 $\frac{1}{2}{{x}^{2}}\sin {{150}^{\circ}}=98-49\sqrt{3}$,故 $a+b+c=150$.

答案
解析
备注