等边三角形 $T$ 内接于半径为10的圆 $A$,半径为3的圆 $B$ 与圆 $A$ 内切三角形 $T$ 的一个顶点处,半径都为2的圆 $C$ 和圆 $D$ 与圆 $A$ 内切于三角形 $T$ 的另外两个顶点处,圆 $B$、圆 $C$ 和圆 $D$ 都与半径为 $\frac{m}{n}$ 的圆 $E$ 外切,其中 $m$,$n$ 是互素的整数.求 $m+n$.
【难度】
【出处】
2009年第27届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
32
【解析】
如图所示,设圆 $B$,$C$,$D$ 分别与圆 $A$ 相切于点 $X$,$Y$,$Z$,圆 $E$ 的半径为 $r$.因为圆 $C$ 和圆 $D$ 是等圆,故点 $E$ 位于圆 $A$ 的过点 $X$ 的直径上,注意到 $AC=8$,$AE\text{=}r-4$,$CE=r+2$ 且 $\angle CAE={{60}^{\circ }}$,由余弦定理可知,${{\left( r-4 \right)}^{2}}+{{8}^{2}}-2\left( r-4\right)\cdot 8\cdot \cos {{60}^{\circ }}\text{=}{{\left( r+2 \right)}^{2}}$.展开并整理,可求出 $r=\frac{27}{5}$.故 $m+n=27+5=32$.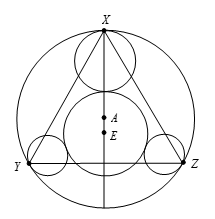

答案
解析
备注