设 $MN=1$ 是圆的直径,$A$,$B$ 是此圆半圆弧上的两点且 $A$ 是该半圆弧的中点,$MB=\frac{3}{5}$.点 $C$ 位于另一半圆弧上.设直径 $MN$ 与弦 $AC$,$BC$ 的交点间的线段长为 $d$.若 $d$ 这的最大值可以写为 $r-s\sqrt{t}$ 的形式,其中 $r s t$ 是正整数且 $t$ 不被任何素数的平女整除,求 $r+s+t$.
【难度】
【出处】
2009年第27届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
14
【解析】
用 $\left[ XYZ \right]$ 表示 $\vartriangle XYZ$ 的面积.如图所示,设 $BC$,$AC$ 分别与 $MN$ 交于点 $P$,$Q$,$\frac{CM}{Cn}=x$,则 $\frac{MP}{NP}=\frac{\left[ BMC \right]}{\left[ BNC\right]}=\frac{BM\cdot CM\cdot \sin \angle BMC}{BN\cdot CN\cdot \sin \angle BNC}=\frac{3x}{4}$.因 $NP=1-MP$,故 $MP=\frac{3x}{3x+4}$.同理,$\frac{MQ}{NQ}=\frac{\left[ AMC \right]}{\left[ ANC\right]}=\frac{AM\cdot CM\cdot \sin \angle AMC}{AN\cdot CN\cdot \sin \angle ANC}=x$,可得 $MQ=\frac{x}{x+1}$.而 $MQ-MP=d$,于是 $\frac{x}{x+1}-\frac{3x}{3x+4}=d$,整理得 $3d{{x}^{2}}+\left(7d-1 \right)x+4d=0$.因该方程的判别式非负,故 ${{d}^{2}}-14d+1\geqslant 0$,又 $0d1$,故 $d$ 的最大值为 $7-4\sqrt{3}$,于是 $r+s+t=14$.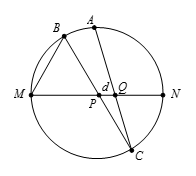

答案
解析
备注