对实数 $a$,令 $\left[ a \right]$ 表示小于或等于 $a$ 的最大整数。设 $R$ 为坐标平面内满足 ${{\left[ x \right]}^{2}}+{{\left[ y \right]}^{2}}=25$ 的点 $\left( x ,y \right)$ 所组成的区域。区域 $R$ 被完全包含在一个半径为 $r$ 的圆盘中(圆盘是指圆周与它内部的点的并集)。 $r$ 的最小值可以表示成 $\frac{\sqrt{m}}{n}$,其中 $m$ 和 $n$ 都是整数且 $m$ 不能被任何素数的平方整除。求 $m+n$ 的值。
【难度】
【出处】
2010年第28届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
132
【解析】
设 $\left( x ,y \right)\in \mathbf{R}$,因为 $\left\lfloor a \right\rfloor $ 是整数且 ${{\left\lfloor x \right\rfloor }^{2}}+{{\left\lfloor y \right\rfloor }^{2}}=25$,所以有序对 $\left(\left\lfloor x \right\rfloor \left\lfloor y \right\rfloor \right)$ 只能是集合 $S=\left\{ \left( \pm 5, 0 \right) ,\left( \pm 4, \pm 3 \right) ,\left( \pm 3 ,\pm 4 \right) ,\left( 0 \pm ,5 \right) \right\}$ 中的元素。这样,$R$ 是12个单位正方形组成的区域的子集(这12个单位正方形的某些边不在 $R$ 中),且 $R$ 的左下角在 $S$ 中,如图所示。
区域 $R$ 关于点 $Q=\left( \frac{1}{2}, \frac{1}{2} \right)$ 对称。点 $A=\left(4 5 \right)$,$B\left( 5, 4 \right)$,$C=\left( -3 ,-4 \right)$,$D\left(-4 ,-3 \right)$ 在区域 $R$ 的边界上。 $ABCD$ 是中心为点 $Q$ 的矩形,能覆盖这四个点(它们是 $R$ 的边界点)的最小的圆是 $ABCD$ 的外接圆,它的直径为 $AC=\sqrt{{{7}^{2}}+{{9}^{2}}}=\sqrt{130}$ 。把这12个单位正方形的顶点代入不等式 ${{\left( x-\frac{1}{2} \right)}^{2}}+{{\left( y-\frac{1}{2}\right)}^{2}}\leqslant \frac{65}{2}$(这个不等式表示的是圆 $Q$ 的圆周及其内部的点)中,得知这个圆覆盖了整个区域 $R$,所以 $r$ 的最小值为 $\frac{\sqrt{130}}{2}$,故 $m+n=132$ 。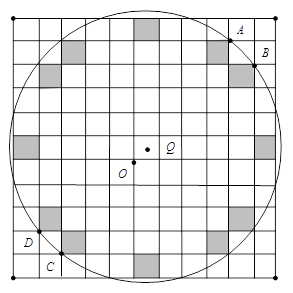
区域 $R$ 关于点 $Q=\left( \frac{1}{2}, \frac{1}{2} \right)$ 对称。点 $A=\left(4 5 \right)$,$B\left( 5, 4 \right)$,$C=\left( -3 ,-4 \right)$,$D\left(-4 ,-3 \right)$ 在区域 $R$ 的边界上。 $ABCD$ 是中心为点 $Q$ 的矩形,能覆盖这四个点(它们是 $R$ 的边界点)的最小的圆是 $ABCD$ 的外接圆,它的直径为 $AC=\sqrt{{{7}^{2}}+{{9}^{2}}}=\sqrt{130}$ 。把这12个单位正方形的顶点代入不等式 ${{\left( x-\frac{1}{2} \right)}^{2}}+{{\left( y-\frac{1}{2}\right)}^{2}}\leqslant \frac{65}{2}$(这个不等式表示的是圆 $Q$ 的圆周及其内部的点)中,得知这个圆覆盖了整个区域 $R$,所以 $r$ 的最小值为 $\frac{\sqrt{130}}{2}$,故 $m+n=132$ 。

答案
解析
备注