矩形 $ABCD$ 和以 $AB$ 为直径的半圆共面且内部不重叠。设 $R$ 为矩形和半圆所围成的区域,直线 $l$ 分别交半圆,线段 $AB$ 和线段 $CD$ 于不同的点 $N$,$U$ 和 $T$ 。直线 $l$ 将区域 $R$ 分成面积比为 $1:2$ 的两部分。若 $AU=84$,$AN=126$,$UB=168$,则 $DA$ 的长度为 $m\sqrt{n}$,其中 $m$、$n$ 是正整数,且 $n$ 不能被任何素数的平方整除。求 $m+n$ 的值。
【难度】
【出处】
2010年第28届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
69
【解析】
如图所示,设线段 $AB$ 的中点为 $O$,则 $AO=\frac{AU+UB}{2}=126=AN$,$UO=42$ 。所以 $\vartriangle AON$ 是等边三角形,$\angle AON={{60}^{\circ }}$,这说明扇形 $AON$ 和 $NOB$ 的面积比为 $1:2$,过点 $U$ 作 $UQ\bot DC$,垂足为 $Q$ 。因为 $\frac{AU}{UB}=\frac{1}{2}$,所以长方形 $AUQD$ 和 $UQCB$ 的面积比为 $1:2$,因为直线 $l$ 将区域 $R$ 分成面积比为 $1:2$ 的两部分,所以 $\vartriangle NUO$ 和 $\vartriangle UQT$ 的面积相等。过点 $N$ 作 $NP\bot AB$,垂足为 $P$ 。注意到 $\vartriangle NUP$ 和 $\vartriangle UTQ$ 相似,且面积比为 $\frac{U{{Q}^{2}}}{N{{P}^{2}}}=\frac{{{S}_{\vartriangle UTQ}}}{{{S}_{\vartriangle NUP}}}=\frac{{{S}_{\vartriangle NOU}}}{{{S}_{\vartriangle NUP}}}=\frac{UO}{UP}$ 。因此 $UQ=NP\cdot \sqrt{\frac{UO}{UP}}$ 。在 $\vartriangle NOP$ 中,$NO=AO=126$,$\angle NPO={{90}^{\circ }}$ 且 $\angle NOP={{60}^{\circ }}$ 。从而 $NP=63\sqrt{3}$,$OP=63$,$UP=OP-UO=21$,故 $\sqrt{\frac{UO}{UP}}=\sqrt{\frac{42}{21}}=\sqrt{2}$ 。所以
$DA=UQ=NP\cdot \sqrt{\frac{UO}{UP}}=63\sqrt{3}$,
从而 $m+n=69$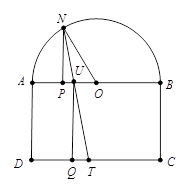
$DA=UQ=NP\cdot \sqrt{\frac{UO}{UP}}=63\sqrt{3}$,
从而 $m+n=69$

答案
解析
备注