在 $\text{Rt}\vartriangle ABC$ 中,$\angle ACB={{90}^{\circ }}$,$\angle BAC{{45}^{\circ }}$,$AB=4$ 。点 $P$ 在边 $AB$ 上,使得 $\angle APC=2\angle ACP$,$CP=1$ 。 $\frac{AP}{BP}$ 可以表示成 $p+q\sqrt{r}$,其中,$p$,$q$,$r$ 是正整数,且 $r$ 不能被任何素数的平方整除。求 $p+q+r$ 的值。
【难度】
【出处】
2010年第28届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
7
【解析】
设 $\vartriangle ABC$ 外接圆的圆心为 $O$,半径为 $r$,且 $\angle ACP=\alpha $,如图所示,延长 $CP$ 交圆 $O$ 于点 $D$ 。因为 $\angle AOD=\angle DPB=2\alpha $,所以 $DO=DP=r$ 。由圆幂定理知 $\frac{CP}{BP}=\frac{AP}{DP}$,$\frac{CP}{AP}=\frac{BP}{DP}$ 。因此 $\frac{CP}{BP}+\frac{CP}{AP}=\frac{AP}{DP}+\frac{BP}{DP}=\frac{AB}{DP}=\frac{2r}{r}=2$ 。条件 $\angle BAC{{45}^{\circ }}$ 说明 $APBP$ 。因为 $CP=1$,前面的等式可化成 $\frac{1}{4-AP}+\frac{1}{AP}=2$,得到 $AP=2+\sqrt{2}$ 。由此可得 $BP=2-\sqrt{2}$,所以 $\frac{AP}{BP}=\frac{2+\sqrt{2}}{2-\sqrt{2}}=3+2\sqrt{2}$ 。从而 $p+q+r=7$ 。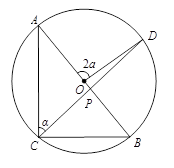

答案
解析
备注