五边形 $ABCDE$ 内接于圆 $O$,$AD=BC=AE$,$BE,CD$ 的中点分别为 $M,N$,$\triangle AMN$ 的重心为 $G$,$CE$ 与 $BD$ 交于点 $P$,$H$ 为 $\triangle AED$ 垂心,设 $OG$ 与 $PH$ 交于 $T$,求证:$AT \perp BC.$ 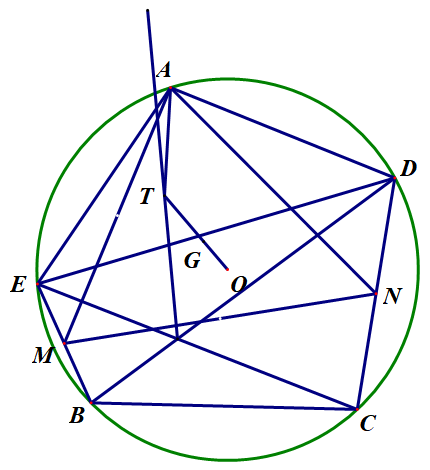

【难度】
【出处】
2019年国家集训队数学试题.day1
【标注】
【答案】
略
【解析】
略
答案
解析
备注