在 $\Delta ABC$ 中,$AB=\frac{20}{11}AC$ 。 $\angle A$ 的角平分线与 $BC$ 边交于点 $D$ 。点 $M$ 是 $AD$ 边中点。点 $P$ 是 $AC$ 与直线 $BM$ 交点。 $\frac{CP}{PA}=\frac{m}{n}$,其中 $m\text{,}n$ 为互质正整数。求 $m+n$ 。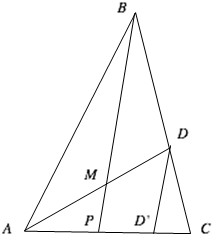

【难度】
【出处】
2011年第29届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
051
【解析】
如图,在 $AC$ 取点 ${D}'$ 使得 $BP\parallel D{D}'$ 。因为 $\Delta BPC\sim \Delta D{D}'C$,于是根据角平分线分线段成比例,$\frac{PC}{{D}'C}=1+\frac{BD}{DC}=1+\frac{AB}{AC}=\frac{31}{11}$ 。由中位线定理,$AP=P{D}'$ 。因此,$\frac{CP}{PA}=\frac{1}{\frac{P{D}'}{PC}}=\frac{1}{1\text{-}\frac{{D}'C}{PC}}=\frac{31}{20}$,则 $m+n\text{=}051$
答案
解析
备注