立方体 $ABCDEFGH$ 如下图所示,棱长为 $1$ 。现有一平面经过顶点 $D$、$AB$ 中点 $M$ 和 $CG$ 中点 $N$ 。该平面将立方体分为两块,两块中较大的体积记为 $\frac{p}{q}$,其中 $p,q$ 为互质的正整数。求 $p+q$ 。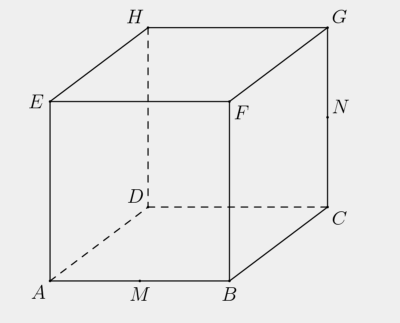

【难度】
【出处】
2012年第30届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
089
【解析】
以 $D$ 为坐标原点 $C,A,H$ 分别在 $x\text{,}y\text{,}z$ 轴上建立空间直角坐标系。 $D\text{=}\left(000 \right)M\text{=}\left( 0.510 \right)N\text{=}\left( 10\text{,}0.5 \right)$ 。过 $D,M,N$ 的平面方程为 $2x-y-4z\text{=}0$ 。令 $Q=\left(1,1,0.25 \right)$ 为该平面与 $BF$ 的交点,令 $p\text{=}\left( 1\text{,}2\text{,}0 \right)$,则 $P$ 在该平面上,且在线段 $DM,NQ,CB$ 的延长线上。所以四面体 $DPCN=DMBCQN+MPBQ$ 是一个直三棱锥。因为三棱锥 $MPBQ$ 和三棱锥 $DPCN$ 相似且相似比为 $5$ 。所以 $DMBCQN$ 的体积为 $\left[DPCN \right]-\left[ MPBQ \right]=\left[ DPCN \right]-{{\left( \frac{1}{2}\right)}^{3}}\left[ DPCN \right]=\frac{7}{8}\left[ DPCN \right]$ 。 $DPCN$ 是底面边长为 $1$ 高为 $5$ 的直三棱锥,所以 $\left[DPCN \right]=\frac{1}{3}\cdot 1\cdot 0.5=\frac{1}{6},\left[ DMBCQN\right]=\frac{7}{8}\cdot \frac{1}{6}=\frac{7}{48}$ 。因为该体积小于 $0.5$,所求为剩余部分体积 $\left[ABCDEFGH \right]-\left[ DMBCQN \right]=1-\frac{7}{48}=\frac{41}{48}\top+q\text{=}089$
答案
解析
备注