Ana,Bob,Cao分别以 $8.6m/s\text{,}6.2m/s\text{,}5m/s$ 的速度匀速骑行。他们同时从一矩形场地的东北角出发。该场地长边是东西向的。Ana向西出发并且沿场地边骑行,Bob向南出发沿场地边骑行,Cao沿直线向场地南侧边上一点 $D$ 骑行。Cao到达 $D$ 点时,恰好Ana和Bob也第一次到达 $D$ 点。场地的长、宽和点 $D$ 到场地东南角的距离之比可写作 $p\text{:}q\text{:}r$,其中 $p\text{,}q\text{,}r$ 是正整数且 $p\text{,}q$ 互质。求 $p+q+r$ 。
【难度】
【出处】
2012年第30届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
061
【解析】
如图,注意到 $\frac{2a+b+c}{8.6}\text{=}1\text{,}\frac{b+c}{6.2}\text{=}1$ 。两式相减得到 $a\text{=}1.2$ 。因为 $\frac{\sqrt{{{b}^{2}}+{{c}^{2}}}}{5}\text{=}1\text{,}b+c\text{=}6.2$ 。解得 $\left\{ \begin{matrix}
& b+c\text{=}6.2 \\
& b-c\text{=}3.4 \\
\end{matrix}\right.\Rightarrow \left\{ \begin{matrix}& b\text{=}4.8 \\
& c\text{=}1.4 \\
\end{matrix}\right.$,因此我们所求比例为 $1.4\text{:}6\text{:}4.8\text{=}7\text{:}30\text{:}24$,所求值为 $7+30+24\text{=}061$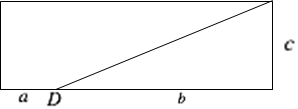
& b+c\text{=}6.2 \\
& b-c\text{=}3.4 \\
\end{matrix}\right.\Rightarrow \left\{ \begin{matrix}& b\text{=}4.8 \\
& c\text{=}1.4 \\
\end{matrix}\right.$,因此我们所求比例为 $1.4\text{:}6\text{:}4.8\text{=}7\text{:}30\text{:}24$,所求值为 $7+30+24\text{=}061$

答案
解析
备注