在下图中,外部的正方形 $S$ 边长为40。较小的正方形 ${S}'$ 边长为15,与大正方形有相同的中心且对应边平行。 $S$ 各边的中点分别与和它们最近的 ${S}'$ 的两个顶点相连,形成了图中所示的内接于 $S$ 的四角星。将四角星剪下并以 ${S}'$ 为底面折叠成四棱锥。求该四棱锥的体积。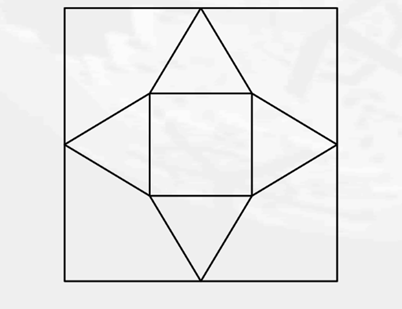

【难度】
【出处】
2012年第30届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
750
【解析】
四棱锥的体积为 $V\text{=}\frac{1}{3}bh$,其中 $b$ 是底面面积,$h$ 是高。则 $b\text{=}{{15}^{2}}\text{=}225$ 。设四个小三角形的高为 ${h}'$ 。观察可得 $40\text{=}2{h}'+15\Rightarrow {h}'\text{=}12.5$ 。再由毕达哥拉斯定理,$h\text{=}\sqrt{{{12.5}^{2}}-{{7.5}^{2}}}\text{=}\sqrt{100}\text{=}10$ 。故 $V\text{=}\frac{1}{3}bh\text{=}750$
答案
解析
备注