运动鞋系带的 $8$ 个小孔在矩形的一对长边上,每个长边上各均匀排列 $4$ 个小孔。该矩形长 $80mm$,宽 $50mm$ 。矩形的四个顶点分别有一个小孔。如下图所示,鞋带须穿过矩形一宽边两端的小孔然后交叉穿过对边上相继的小孔直到穿到另一宽边两端的小孔。穿过所有小孔之后,鞋带两端需各剩余至少 $200mm$ 以便打结。求鞋带长度最少多少厘米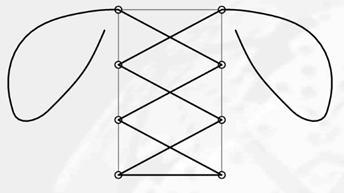

【难度】
【出处】
2014年第32届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
790
【解析】
矩形被分为长 $\frac{80}{3}mm$ 宽 $50mm$ 的三个小矩形。根据毕达哥拉斯定理,小矩形的对角线为 $\sqrt{{{50}^{2}}+{{\left( \frac{80}{3}\right)}^{2}}}\text{=}\frac{170}{3}mm$,因为一共包含 $6$ 条对角线、$1$ 条宽和两端各 $200mm$ 的剩余,所以鞋带最短长度为 $6\times\frac{170}{3}+50+200\times 2\text{=}790$
答案
解析
备注