如图1(1),一个矩形的边长分别为 $a$ 与 $36$ 。在矩形的每个顶点与长为 $36$ 的边的中点处各装了一个铰链,将长为 $a$ 的边向下压,在压的过程中保持长为 $a$ 的边互相平行,得到一个如图1(2)所示的凸六边形。当这两个六边形的长为 $a$ 的边互相平行,且距离为 $24$ 时,六边形的面积与原来的矩形面积相等,求 ${{a}^{2}}$ 的值。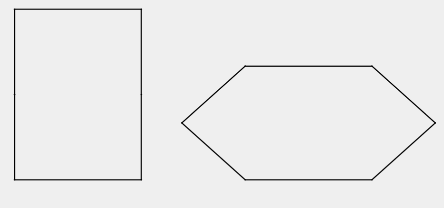

【难度】
【出处】
2014年第32届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
720
【解析】
如图,我们将六边形分为左右两个等腰三角形和中间的矩形。由海伦公式,两侧的等腰三角形面积为 $\sqrt{30\cdot12\cdot 12\cdot 6}\text{=}\sqrt{180\cdot {{12}^{2}}}\text{=}72\sqrt{5}$ 。中间矩形的面积 $24a$ 。原矩形面积为 $36a$ 。则 $24a+144\sqrt{5}\text{=}36a\Rightarrow12a\text{=}144\sqrt{5}\Rightarrow a\text{=}12\sqrt{5}\Rightarrow{{a}^{2}}\text{=}720$

答案
解析
备注