一个半径 $4$ 英尺,高 $10$ 英尺的圆柱形桶装满水。一个棱长 $8$ 英尺的实心立方体被置于桶口使得其对角线垂直于地面。放置立方体后溢出的水量为 $v$ 立方英尺。求 ${{v}^{\text{2}}}$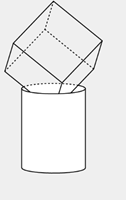

【难度】
【出处】
2015年第33届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
384
【解析】
圆柱的顶部的圆周与立方体三条棱交于三点,由对称性知这三点是等边三角形的三个顶点。因为圆半径为 $4$,所以等边三角形边长为 $s\text{=}4\sqrt{3}$ 。我们所求部分是以该等边三角形为底面的正三棱锥,且其余三个面均为等腰直角三角形,腰长为 $\frac{4\sqrt{3}}{\sqrt{2}}\text{=}2\sqrt{6}$ 。于是体积 $v\text{=}\frac{1}{3}\cdot2\sqrt{6}\cdot \left( \frac{1}{2}\cdot {{\left( 2\sqrt{6} \right)}^{2}}\right)\text{=}8\sqrt{6}\Rightarrow {{v}^{2}}\text{=}384$
答案
解析
备注