圆 $P$ 和圆 $Q$ 半径分别为 $1,4$,并且两圆外切于点 $A$ 。点 $B$ 在圆 $P$ 上,点 $C$ 在圆 $Q$ 上,使得 $BC$ 为两圆的外公切线段。过 $A$ 的直线 $l$ 交圆 $P$ 于另一点 $D$ 并且交圆 $Q$ 于另一点 $E$ 。 $B,C$ 在该直线同侧,并且 $\Delta DBA$ 和 $\Delta ACE$ 面积相等。两三角形的面积为 $\frac{m}{n}$,其中 $m\text{,}n$ 为互质的正整数。求 $m+n$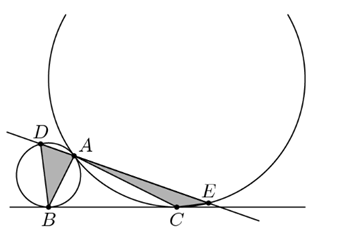

【难度】
【出处】
2015年第33届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
129
【解析】
设 ${{O}_{1}},{{O}_{2}}$ 分别为圆心,并如图延长 $CB,{{O}_{1}}{{O}_{2}}$ 相较于 $N$ 。过 $B$ 作 ${{O}_{1}}N$ 垂线,过 $C$ 作 ${{O}_{2}}N$ 垂线,垂足分别记为 $K,L$
。设 $N{{O}_{1}}=k$,由 $\Delta {{O}_{1}}BN\tilde{ }\Delta {{O}_{2}}CN$,$\frac{k+5}{k}\text{=}\frac{4}{1}\Rightarrow k\text{=}\frac{5}{3}$ 。不难得到 $AK=AL=\frac{24}{15},BK=\frac{12}{15},CL=\frac{48}{15}$ 。以 $A$ 为原点,$\overrightarrow{{{O}_{1}}{{O}_{2}}}$ 为 $x$ 轴正方向建立平面直角坐标系。因为 $\Delta A{{O}_{1}}D\tilde{ }\Delta A{{O}_{2}}E$,所以 $\frac{DA}{AE}=\frac{{{O}_{1}}A}{{{O}_{2}}A}=\frac{1}{4}$ 。设直线 $l$ 方程为 $y\text{=}-mx\Rightarrow mx+y\text{=}0\text{,}m\in \mathbb{R}$ 。坐标系中 $A\text{=}\left( 0\text{,}0\right),B\text{=}\left( {{x}_{B}}\text{,}{{y}_{B}} \right)\text{=}\left(\frac{-24}{15}\text{,}\frac{-12}{15} \right),C\text{=}\left({{x}_{C}}\text{,}{{y}_{C}} \right)\text{=}\left(\frac{24}{15}\text{,}\frac{-48}{15} \right)$ 。由点到直线距离公式有 $\left|\frac{m{{x}_{B}}+1\left( {{y}_{B}} \right)+0}{\sqrt{{{m}^{2}}+1}}\right|\text{=}\frac{4\left| m{{x}_{C}}+1\left( {{y}_{C}} \right)+0\right|}{\sqrt{{{m}^{2}}+1}}\Rightarrow \left| m{{x}_{B}}+{{y}_{B}}\right|\text{=}4\left| m{{x}_{C}}+{{y}_{C}} \right|\Rightarrow \left|\frac{-24m}{15}+\frac{-12}{15} \right|\text{=}4\left|\frac{24m}{15}+\frac{-48}{15} \right|$ 若 $m\text{}2$,显然 $B,C$ 不在直线 $l$ 同侧。又因为 $m>0$,含绝对值等式可变为 $\frac{6m}{15}+\frac{3}{15}\text{=}\frac{48}{15}-\frac{24m}{15}\Rightarrow2m\text{=}3\Rightarrow m\text{=}\frac{3}{2}$ 。于是 $l\text{:}y\text{=}-\frac{3}{2}x$ 。联立直线和圆的方程可解得 $D\text{=}\left({{x}_{0}}\text{,}{{y}_{0}} \right)\text{,}{{y}_{D}}\text{=}\frac{12}{13}$ 。所以 $D,A$ 的距离为 $\frac{4}{\sqrt{13}}$ 。 $B$ 到 $AD$ 距离为 $\frac{\left|\frac{3}{2}\cdot \frac{-24}{15}+\frac{-12}{15}+0 \right|}{\sqrt{{{\left(\frac{3}{2}\right)}^{2}}+1}}\text{=}\frac{\frac{48}{15}}{\frac{\sqrt{13}}{2}}\text{=}\frac{32}{5\sqrt{13}}$ 。所以所求面积为 $\frac{1}{2}\left(\frac{32}{5\sqrt{13}}\frac{4}{\sqrt{13}} \right)=\frac{64}{65}$,于是 $m+n\text{=}64+65\text{=}129$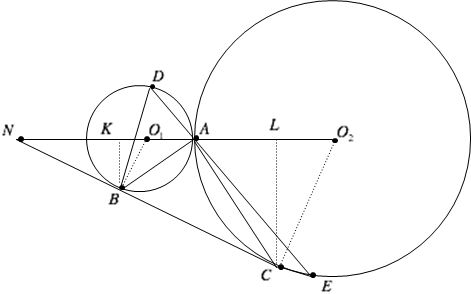
。设 $N{{O}_{1}}=k$,由 $\Delta {{O}_{1}}BN\tilde{ }\Delta {{O}_{2}}CN$,$\frac{k+5}{k}\text{=}\frac{4}{1}\Rightarrow k\text{=}\frac{5}{3}$ 。不难得到 $AK=AL=\frac{24}{15},BK=\frac{12}{15},CL=\frac{48}{15}$ 。以 $A$ 为原点,$\overrightarrow{{{O}_{1}}{{O}_{2}}}$ 为 $x$ 轴正方向建立平面直角坐标系。因为 $\Delta A{{O}_{1}}D\tilde{ }\Delta A{{O}_{2}}E$,所以 $\frac{DA}{AE}=\frac{{{O}_{1}}A}{{{O}_{2}}A}=\frac{1}{4}$ 。设直线 $l$ 方程为 $y\text{=}-mx\Rightarrow mx+y\text{=}0\text{,}m\in \mathbb{R}$ 。坐标系中 $A\text{=}\left( 0\text{,}0\right),B\text{=}\left( {{x}_{B}}\text{,}{{y}_{B}} \right)\text{=}\left(\frac{-24}{15}\text{,}\frac{-12}{15} \right),C\text{=}\left({{x}_{C}}\text{,}{{y}_{C}} \right)\text{=}\left(\frac{24}{15}\text{,}\frac{-48}{15} \right)$ 。由点到直线距离公式有 $\left|\frac{m{{x}_{B}}+1\left( {{y}_{B}} \right)+0}{\sqrt{{{m}^{2}}+1}}\right|\text{=}\frac{4\left| m{{x}_{C}}+1\left( {{y}_{C}} \right)+0\right|}{\sqrt{{{m}^{2}}+1}}\Rightarrow \left| m{{x}_{B}}+{{y}_{B}}\right|\text{=}4\left| m{{x}_{C}}+{{y}_{C}} \right|\Rightarrow \left|\frac{-24m}{15}+\frac{-12}{15} \right|\text{=}4\left|\frac{24m}{15}+\frac{-48}{15} \right|$ 若 $m\text{}2$,显然 $B,C$ 不在直线 $l$ 同侧。又因为 $m>0$,含绝对值等式可变为 $\frac{6m}{15}+\frac{3}{15}\text{=}\frac{48}{15}-\frac{24m}{15}\Rightarrow2m\text{=}3\Rightarrow m\text{=}\frac{3}{2}$ 。于是 $l\text{:}y\text{=}-\frac{3}{2}x$ 。联立直线和圆的方程可解得 $D\text{=}\left({{x}_{0}}\text{,}{{y}_{0}} \right)\text{,}{{y}_{D}}\text{=}\frac{12}{13}$ 。所以 $D,A$ 的距离为 $\frac{4}{\sqrt{13}}$ 。 $B$ 到 $AD$ 距离为 $\frac{\left|\frac{3}{2}\cdot \frac{-24}{15}+\frac{-12}{15}+0 \right|}{\sqrt{{{\left(\frac{3}{2}\right)}^{2}}+1}}\text{=}\frac{\frac{48}{15}}{\frac{\sqrt{13}}{2}}\text{=}\frac{32}{5\sqrt{13}}$ 。所以所求面积为 $\frac{1}{2}\left(\frac{32}{5\sqrt{13}}\frac{4}{\sqrt{13}} \right)=\frac{64}{65}$,于是 $m+n\text{=}64+65\text{=}129$

答案
解析
备注