某俱乐部共有 $99$ 名成员,每一个成员都声称只愿意和自己认识的人一起打桥牌.已知每个成员都至少认识 $67$ 名成员.证明一定有 $4$ 名成员,他们可以在一起打桥牌?
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
做一个图 $G$:用 $99$ 个点表示 $99$ 名成员,如果两名成员相互认识,就在相应的两个顶点之间连一条边.已知条件是:对任意顶点 $v$,$d(v)\geqslant 67$.欲证明 $G$ 中含有一个 $4$ 阶完全图 $K_4$.
在 $G$ 中任取一个顶点 $u$,由于 $d(u)\geqslant 67$,所以存在顶点 $v$,使得与 $v$ 相邻且与 $u$ 不相邻的顶点至多为 $99-1-67=31$ 个.同样,与 $v$ 不相邻且与 $u$ 相邻的顶点也至多 $31$ 个.于是图 $G$ 中至少有 $99-31-31-2-35$ 个顶点和 $u,v$ 均相邻.如图所示,设顶点 $x$ 和顶点 $u,v$ 相邻.
由于 $d(x)\geqslant 67$,并且 $G$ 中至多只有 $31+31+2=64$ 个不同时和 $u,v$ 均相邻的顶点,因此顶点 $x$ 至少还和一个与 $u,v$ 均相邻的顶点 $y$ 相邻.从而 $u,v,x,y$ 是 $4$ 个两两相邻的顶点.于是命题得证.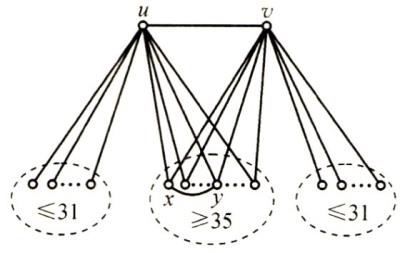
在 $G$ 中任取一个顶点 $u$,由于 $d(u)\geqslant 67$,所以存在顶点 $v$,使得与 $v$ 相邻且与 $u$ 不相邻的顶点至多为 $99-1-67=31$ 个.同样,与 $v$ 不相邻且与 $u$ 相邻的顶点也至多 $31$ 个.于是图 $G$ 中至少有 $99-31-31-2-35$ 个顶点和 $u,v$ 均相邻.如图所示,设顶点 $x$ 和顶点 $u,v$ 相邻.
由于 $d(x)\geqslant 67$,并且 $G$ 中至多只有 $31+31+2=64$ 个不同时和 $u,v$ 均相邻的顶点,因此顶点 $x$ 至少还和一个与 $u,v$ 均相邻的顶点 $y$ 相邻.从而 $u,v,x,y$ 是 $4$ 个两两相邻的顶点.于是命题得证.

答案
解析
备注