直角三角形边长为 $2\sqrt{3}\text{,}5\sqrt{37}$,顶点分别在三条边上的内接正三角形(如下图所示)的面积最大值为 $\frac{m\sqrt{p}}{n}$,其中 $m\text{,}n\text{,}p$ 均为正整数,$m\text{,}n$ 互质,$p$ 不含平方因子。求 $m+n+p$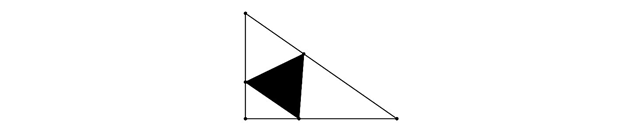

【难度】
【出处】
2017年第35届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
145
【解析】
【引理】若 $x\text{,}y$ 满足 $px+qy\text{=}1$,则 $\sqrt{{{x}^{2}}+{{y}^{2}}}$ 的最小值为 $\frac{1}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ 。 【证明】:点 $\left({{x}_{0}}\text{,}{{y}_{0}} \right)$ 到直线 $px+qy-1\text{=}0$ 的距离为 $\frac{\left|p{{x}_{0}}+q{{y}_{0}}-1 \right|}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ 。则原点到直线上的点 $\left(x\text{,}y \right)$ 距离最小值为 $\frac{1}{\sqrt{{{p}^{2}}+{{q}^{2}}}}$ 。 设直角三角形顶点坐标分别为 $\left(0\text{,}0 \right)\text{,}\left( 5\text{,}0 \right)\text{,}\left(0\text{,}2\sqrt{3} \right)$,设 $\left( a\text{,}0 \right)\text{,}\left(0\text{,}b \right)$ 是等边三角形的两个顶点。则等边三角形剩余的顶点为 $\left(\frac{a+\sqrt{3}b}{2}\text{,}\frac{\sqrt{3}a+b}{2} \right)$,该顶点在直线 $\frac{x}{5}+\frac{y}{2\sqrt{3}}\text{=}1$ 。于是代入得到 $\frac{7}{20}a+\frac{11\sqrt{3}}{60}b\text{=}1$ 。根据引理,$\sqrt{{{a}^{2}}+{{b}^{2}}}$ 最小值为 $\frac{1}{\sqrt{{{\left(\frac{7}{20} \right)}^{2}}+{{\left( \frac{11\sqrt{3}}{60}\right)}^{2}}}}\text{=}\frac{10\sqrt{3}}{\sqrt{67}}$ 。所以等边三角形面积最小值为 $\frac{\sqrt{3}}{4}\cdot{{\left( \frac{10\sqrt{3}}{\sqrt{67}} \right)}^{2}}=\frac{75\sqrt{3}}{67}$,所求值为 $75+3+67\text{=}145$
答案
解析
备注