一三角形的顶点为 $A\left( 0\text{,}0 \right)\text{,}B\left( 12\text{,}0 \right),C\left( 8\text{,}10 \right)$ 。在三角形内部随机选取一点,该点满足到 $B$ 的距离近于 $A,C$ 距离的概率为 $\frac{p}{q}$,其中 $p\text{,}q$ 是互质正整数。求 $p+q$
【难度】
【出处】
2017年第35届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
409
【解析】
如图,到 $B$ 距离小于到 $A$ 距离的点在 $AB$ 垂直平分线的右侧,即在 $PZ$ 右侧。
到 $B$ 距离小于到 $C$ 距离的点在 $PX$ 下侧。因此三角形内到 $B$ 距离小于到 $A,C$ 距离的点集边界为 $BXPZ$ 。因为 $X,Z$ 分别为 $BC,AB$ 中点,所以 $X\text{=}\left(10\text{,}5 \right)\text{,}Z\text{=}\left( 6\text{,}0 \right)$ 。 $PX$ 方程为 $y=\frac{2}{5}x+1$,$PZ$ 方程为 $x=6$ 。所以解得 $P$ 点坐标为 $\left( \text{6},\frac{\text{17}}{\text{5}} \right)$ 。四边形 $BXPZ$ 的面积为 $\frac{\text{109}}{\text{5}}$,三角形 $ABC$ 的面积为 $\text{60}$ 。故所求概率为 $\frac{\frac{\text{109}}{\text{5}}}{\text{60}}\text{=}\frac{\text{109}}{\text{300}}$,所求值为 $1\text{09+300=409}$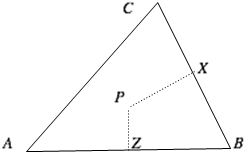
到 $B$ 距离小于到 $C$ 距离的点在 $PX$ 下侧。因此三角形内到 $B$ 距离小于到 $A,C$ 距离的点集边界为 $BXPZ$ 。因为 $X,Z$ 分别为 $BC,AB$ 中点,所以 $X\text{=}\left(10\text{,}5 \right)\text{,}Z\text{=}\left( 6\text{,}0 \right)$ 。 $PX$ 方程为 $y=\frac{2}{5}x+1$,$PZ$ 方程为 $x=6$ 。所以解得 $P$ 点坐标为 $\left( \text{6},\frac{\text{17}}{\text{5}} \right)$ 。四边形 $BXPZ$ 的面积为 $\frac{\text{109}}{\text{5}}$,三角形 $ABC$ 的面积为 $\text{60}$ 。故所求概率为 $\frac{\frac{\text{109}}{\text{5}}}{\text{60}}\text{=}\frac{\text{109}}{\text{300}}$,所求值为 $1\text{09+300=409}$

答案
解析
备注