$ABCDEF$ 是内角相等的六边形，其中 $AB=6,BC=8,CD=10,DE=12$ 。 为可置于该六边形内的圆直径的最大值。求 ${{d}^{2}}$
【难度】
【出处】
2018年第36届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
147
【解析】
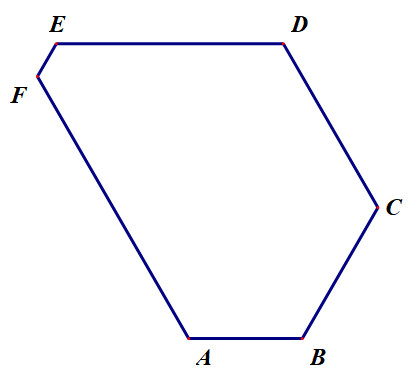由图不难发现 $EF=2,FA=16$ 。再由 $AF,CD$边的限制，圆直径最大值为 $7\sqrt{3}$，${{d}^{2}}\text{=}147$
答案
解析
备注
