求最小的正整数 $n$，使当以任意方式将 $K_n$ 二染色，总存在两个单色三角形，二者恰有一条公共边．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图（a）（b）中，为了清楚起见，我们把蓝线和红线分别画在两个图中，易见图中有 $6$ 蓝 $6$ 红共 $12$ 个单色三角形，图中 $36$ 条边，恰好每边都是一个单色三角形的一条边，任何两个单色三角形都没有公共边，可见所求最小正整数 $n\geqslant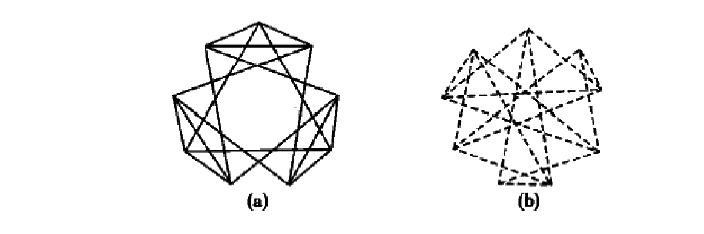 10$．
另一方面，在 $2$ 色 $K_{10}$ 中假设单色三角形有 $p$ 个，非单色三角形有 $q$ 个，则 $p+q=C_{10}^3$．再设从第 $i$ 个顶点 $p_i$ 出发有 $x_i$ 条红边，$9-x_i$ 条蓝边 $(i=1,2,\cdots,10)$，于是图中共有 $\sum_{i=1}^{10}x_i(9-x_i)$ 个两边不同色的异色角，每个非单色三角形内恰有 $2$ 个异色角，所以 $2q=\sum_{i=1}^{10}x_i(9-x_i)$，因为 $x_i(9-x_i)\leqslant (\dfrac{x_i+9-x_i}{2})^2=\dfrac{81}{4}=20\dfrac{1}{4}$，且 $x_i(9-x_i)$ 为整数，所以 $x_i(9-x_i)\leqslant 20$，故 $q=\dfrac{1}{2}\sum_{i=1}^{10}x_{i}(9-x_i)\leqslant \dfrac{1}{2}\times 10\times 20=100$，于是 $p=C_{10}^3-q\ge120-100=20$，即图中至少有 $20$ 个单色三角形，每个三角形有 $3$ 条边，一共至少有 $60$ 条边，但 $K_{10}$ 中只有 $C_{10}^2=45$ 条线段，故必有两个单色三角形恰有一条公共边．综上可知，所求最小正整数 $n=10$．
另一方面，在 $2$ 色 $K_{10}$ 中假设单色三角形有 $p$ 个，非单色三角形有 $q$ 个，则 $p+q=C_{10}^3$．再设从第 $i$ 个顶点 $p_i$ 出发有 $x_i$ 条红边，$9-x_i$ 条蓝边 $(i=1,2,\cdots,10)$，于是图中共有 $\sum_{i=1}^{10}x_i(9-x_i)$ 个两边不同色的异色角，每个非单色三角形内恰有 $2$ 个异色角，所以 $2q=\sum_{i=1}^{10}x_i(9-x_i)$，因为 $x_i(9-x_i)\leqslant (\dfrac{x_i+9-x_i}{2})^2=\dfrac{81}{4}=20\dfrac{1}{4}$，且 $x_i(9-x_i)$ 为整数，所以 $x_i(9-x_i)\leqslant 20$，故 $q=\dfrac{1}{2}\sum_{i=1}^{10}x_{i}(9-x_i)\leqslant \dfrac{1}{2}\times 10\times 20=100$，于是 $p=C_{10}^3-q\ge120-100=20$，即图中至少有 $20$ 个单色三角形，每个三角形有 $3$ 条边，一共至少有 $60$ 条边，但 $K_{10}$ 中只有 $C_{10}^2=45$ 条线段，故必有两个单色三角形恰有一条公共边．综上可知，所求最小正整数 $n=10$．
答案
解析
备注
