求最小的正整数 $n$，使得由 $10$ 个顶点，$n$ 条边的二染色简单图中，总存在单色三角形或单色四边形（即含 $4$ 条线段的圈）．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
图中有 $10$ 个顶点和 $30$ 条边，其中红边（实线）和蓝边（虚线）各 $15$ 条，图中既无单色三角形也无单色四边形，故所求最小正整数 $\geqslant 31$．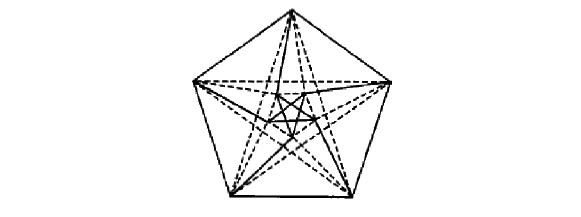
下面证明当 $n=31$ 时，图中必存在单色三角形或单色四边形，由抽屉原理，图中必有 $[\dfrac{31-1}{2}]+1=16$ 条边同色，于是只需证明在 $10$ 个顶点 $16$ 条边的简单图中必存在三角形或四边形．
由于 $16$ 条边有 $32$ 个顶点，故必有一个顶点至多引出 $3$ 条线，不妨设 $A_{10}$ 至多引出 $3$ 条线．于是，除 $A_{10}$ 外其他 $9$ 个顶点至少引出 $16-3=13$ 条线段，$13$ 条线段只有 $26$ 个端点（多余的线段山丘，不影响后面的证明），于是必有一个顶点至多引出 $2$ 条线，不妨设 $A_9$ 引出 $2$ 条线，于是 $8$ 个顶点 $\{A_1,A_2,\cdots,A_8\}$ 个顶点的子图中有 $11$ 条边，以及 $22$ 个端点，故其中必有一个顶点至多引出 $2$ 条线，不妨设 $A_8$ 引出 $2$ 条线，于是以 $\{A_1,A_2,\cdots,A_7\}$ 为顶点的子图中有 $9$ 条边，类似地，以 $\{A_1,A_2,\cdots,A_6\}$ 为顶点的子图中必有 $7$ 条边．因为 $7>6-1$，故这个简单图不是树，其中必有圈．若边数最多的圈有 $6$ 条边，则另外两条边或者圈外有一个公共端点，或者其中至少有一条是连接圈上的两点，无论哪种情形都导致形成三角形或四边形；若边数最多的边至多有 $4$ 条边，结论显然成立．综上可知，所求最小正整数 $n=31$．
下面证明当 $n=31$ 时，图中必存在单色三角形或单色四边形，由抽屉原理，图中必有 $[\dfrac{31-1}{2}]+1=16$ 条边同色，于是只需证明在 $10$ 个顶点 $16$ 条边的简单图中必存在三角形或四边形．由于 $16$ 条边有 $32$ 个顶点，故必有一个顶点至多引出 $3$ 条线，不妨设 $A_{10}$ 至多引出 $3$ 条线．于是，除 $A_{10}$ 外其他 $9$ 个顶点至少引出 $16-3=13$ 条线段，$13$ 条线段只有 $26$ 个端点（多余的线段山丘，不影响后面的证明），于是必有一个顶点至多引出 $2$ 条线，不妨设 $A_9$ 引出 $2$ 条线，于是 $8$ 个顶点 $\{A_1,A_2,\cdots,A_8\}$ 个顶点的子图中有 $11$ 条边，以及 $22$ 个端点，故其中必有一个顶点至多引出 $2$ 条线，不妨设 $A_8$ 引出 $2$ 条线，于是以 $\{A_1,A_2,\cdots,A_7\}$ 为顶点的子图中有 $9$ 条边，类似地，以 $\{A_1,A_2,\cdots,A_6\}$ 为顶点的子图中必有 $7$ 条边．因为 $7>6-1$，故这个简单图不是树，其中必有圈．若边数最多的圈有 $6$ 条边，则另外两条边或者圈外有一个公共端点，或者其中至少有一条是连接圈上的两点，无论哪种情形都导致形成三角形或四边形；若边数最多的边至多有 $4$ 条边，结论显然成立．综上可知，所求最小正整数 $n=31$．
答案
解析
备注
