如图,点 $A$,$B$,$C$,$D$ 和 $E$ 均匀排列在圆的劣弧上。点 $E$,$F$,$G$,$H$,$I$ 和 $A$ 均匀排列在另一以 $C$ 为圆心的劣弧上。 $\angle ABD - \angle AHG = 12^\circ $ 。求 $\angle BAG$ 的角度。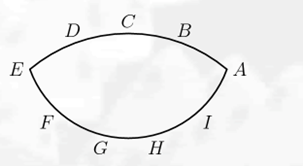

【难度】
【出处】
2015年第33届美国数学邀请赛Ⅰ(AIMEⅠ)
【标注】
【答案】
058
【解析】
设 $ABCDE$ 外接圆圆心为 $O$ 。设圆 $O$ 上的弧 $ED,DC,CB,BA$ 对应角度均 $x$,圆 $C$ 上的弧 $EF,FG,GH,HI,IA$ 的角度均为 $y$ 。则 $\angle ECA\text{=}180-2x\text{=}5y$(1),$\angle ABD\text{=}180-\frac{3x}{2},\angle AHG=180-\frac{3y}{2}$ 。于是有 $180-\frac{3x}{2}=180-\frac{3y}{2}+12$(2)。联立(1),(2)两式得到 $x=20,y=28$ 。 $\angle BAG\text{=}\angle BAE+\angle EAG\text{=}\frac{3x}{2}+y\text{=}058$
答案
解析
备注