如图，$ABCD$ 为正方形。点 $E$ 是 $\overline {AD} $ 中点。点 $F$ 和 $G$ 在 $\overline{CE} $ 上，点 $H$ 和 $J$ 分别在 $\overline {AB} $ 和 $\overline {BC} $ 上，使得 $FGHJ$ 是正方形。点 $K$ 和 $L$ 在 $\overline {GH} $ 上，$M$ 和 $N$ 分别在 $\overline {AD} $ 和 $\overline {AB} $ 上，使得 $KLMN$ 是正方形。 $KLMN$ 的面积是99。求 $FGHJ$ 的面积。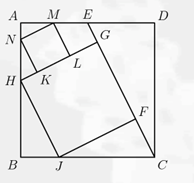
【难度】
【出处】
2015年第33届美国数学邀请赛Ⅰ（AIMEⅠ）
【标注】
【答案】
539
【解析】
设 $ED\text{=}a$，则 $DC=2a\text{.}EC\text{=}\sqrt{5}a$ 。因为 $\angle DCE+\angle FCJ={{90}^{{}^\circ }}$，$\Delta CDE\tilde{ }\Delta JFC$，同理可得其余若干组相似三角形。设 $FGHJ$ 边长为 $b$，则 $JC\text{=}\sqrt{5}\cdot FC=\sqrt{5}\cdot F\dfrac J 2 =\frac{b\sqrt{5}}{2},BJ=\frac{1}{\sqrt{5}},HJ=\frac{b}{\sqrt{5}}$ 。因为 $BC=CJ+BJ$，$2a\text{=}\frac{b\sqrt{5}}{2}+\frac{b}{\sqrt{5}}\Rightarrow b\text{=}\frac{4a\sqrt{5}}{7}$ 。
因为 $\left[ KLMN \right]\text{=}99$，则 $KL=LM=MN=NK=3\sqrt{11}$ 。过 $E$ 作 $ML$ 的垂线，垂足记为 $P$ 。
可以得到 $AM=2AN=\frac{6\sqrt{11}}{\sqrt{5}}$，$ME=\sqrt{5}MP=\sqrt{5}\cdot \frac{EP}{2}=\sqrt{5}\cdot \frac{LG}{2}=\sqrt{5}\cdot\frac{HG-HK-KL}{2}=\sqrt{5}\cdot\frac{\frac{4a\sqrt{5}}{7}-\frac{9\sqrt{11}}{2}}{2}$ 。因为 $AE=AM+ME$，所以 $\frac{6\sqrt{11}}{\sqrt{5}}+\sqrt{5}\cdot\frac{\frac{4a\sqrt{5}}{7}-\frac{9\sqrt{11}}{2}}{2}=a$ 化简得到 $7\sqrt{11}\text{=}\frac{4a\sqrt{5}}{7}$，我们所求值为 ${{\left(7\sqrt{11} \right)}^{2}}\text{=}539$
因为 $\left[ KLMN \right]\text{=}99$，则 $KL=LM=MN=NK=3\sqrt{11}$ 。过 $E$ 作 $ML$ 的垂线，垂足记为 $P$ 。可以得到 $AM=2AN=\frac{6\sqrt{11}}{\sqrt{5}}$，$ME=\sqrt{5}MP=\sqrt{5}\cdot \frac{EP}{2}=\sqrt{5}\cdot \frac{LG}{2}=\sqrt{5}\cdot\frac{HG-HK-KL}{2}=\sqrt{5}\cdot\frac{\frac{4a\sqrt{5}}{7}-\frac{9\sqrt{11}}{2}}{2}$ 。因为 $AE=AM+ME$，所以 $\frac{6\sqrt{11}}{\sqrt{5}}+\sqrt{5}\cdot\frac{\frac{4a\sqrt{5}}{7}-\frac{9\sqrt{11}}{2}}{2}=a$ 化简得到 $7\sqrt{11}\text{=}\frac{4a\sqrt{5}}{7}$，我们所求值为 ${{\left(7\sqrt{11} \right)}^{2}}\text{=}539$
答案
解析
备注
