$\odot {{O}_{1}}\text{,}\odot {{O}_{2}}$ 相交于 $B,C$ 两点，且 $BC$ 是 $\odot {{O}_{1}}$ 的直径。过点 $C$ 作 $\odot {{O}_{1}}$ 的切线，交 $\odot {{O}_{2}}$ 于另一点 $E$，连结 $CE$ 并延长，交 $\odot {{O}_{2}}$ 于点 $F$ 。设点 $H$ 为线段 $AF$ 内的任意一点，连结 $HE$ 并延长，交 $\odot {{O}_{2}}$ 于点 $G$，连结 $BG$ 并延长，与 $AC$ 的延长线交于点 $D$ 。求证：$\frac{AH}{HF}=\frac{AC}{CD}$ 。
【难度】
【出处】
2002第1届CGMO试题
【标注】
【答案】
略
【解析】
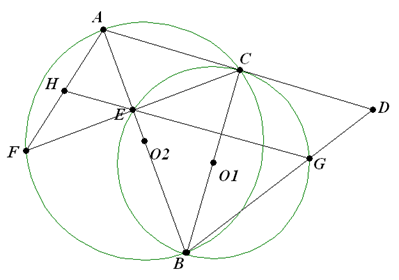如图，因 $BC$ 是 $\odot {{O}_{1}}$ 的直径，$AC$ 与 $\odot {{O}_{1}}$ 切于 $C$，故 $\angle BEC=\angle FEA=\angle BCA=\angle BCD={{90}^{{}^\circ }}$ 。设 $\angle ABC=\alpha,\angle CBD=\beta $，则 $\angle AFC=\alpha ,\angle CEG\text{=}\beta $ 。根据正弦定理，有 $\frac{AH}{\sin\angle HEA}\text{=}\frac{HE}{\sin \angle HAE},\frac{HF}{\sin \angle FEH}=\frac{HE}{\sin \angle HFE}$，即 $\frac{AH}{HE}=\frac{\cos \beta }{\cos \alpha}\text{,}\frac{HF}{HE}\text{=}\frac{\sin \beta }{\sin \alpha }$ 。两式相除得 $\frac{AH}{HF}=\frac{\tan\alpha }{\tan \beta }$（1）。在 $Rt\Delta ABC$ 中，$\frac{AC}{BC}=\tan \alpha $；在 $Rt\Delta BCD$ 中，$\frac{CD}{BC}=\tan \beta$ 。两式相除得 $\frac{AC}{CD}\text{=}\frac{\tan \alpha }{\tan \beta }$（2）。由（1）（2）知，$\frac{AH}{HF}=\frac{AC}{CD}$ 。
答案
解析
备注
