查看数据源：5ca4148f210b28107f52aa11
设 ${{A}_{1}},{{A}_{2}},\cdots ,{{A}_{8}}$ 是平面上任意取定的 $8$ 个点。对平面上任意取定的一条有向直线 $l$，设 ${{A}_{1}},{{A}_{2}},\cdots ,{{A}_{8}}$ 在该直线上的射影分别是 ${{P}_{1}},{{P}_{2}},\cdots ,{{P}_{8}}$ 。如果这 $8$ 个射影两两不重合，依直线 $l$ 的方向依次排列为 ${{P}_{{{i}_{1}}}},{{P}_{{{i}_{2}}}},\cdots ,{{P}_{{{i}_{8}}}}$ 。这样，就得到了 $1\text{,}2\text{,}3\text{,}4\text{,}5\text{,}6\text{,}7\text{,}8$ 的一个排列 ${{i}_{1}}\text{,}{{i}_{2}}\text{,}\cdots \text{,}{{i}_{8}}$（在图1中，此排列为 $2\text{,}1\text{,}8\text{,}3\text{,}7\text{,}4\text{,}6\text{,}5$）。设这 $8$ 个点对平面上所有有向直线作射影后，得到的不同排列的个数为 ${{N}_{8}}\text{=}N\left( {{A}_{1}},{{A}_{2}},\cdots {{A}_{8}} \right)$ 。试求 ${{N}_{8}}$ 的最大值。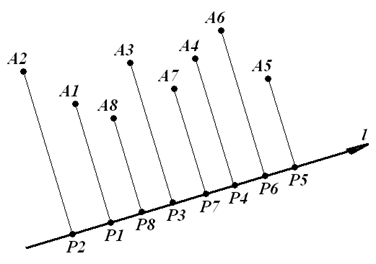
【难度】
【出处】
2002第1届CGMO试题
【标注】
  • 知识点
    >
    二试组合部分
【答案】
${{N}_{\text{8}}}\text{=56}$
【解析】
对两条平行且同方向的有向直线，${{A}_{1}},{{A}_{2}},\cdots,{{A}_{8}}$ 的射影次序一定相同。所以，只要讨论通过一定点 $O$ 的所有有向直线即可。 若所取的有向直线与某两点的连线垂直，则该两点的射影必重合，所以不产生相应的排列。不然，${{A}_{1}},{{A}_{2}},\cdots,{{A}_{8}}$ 的射影必两两不重合，因此，对应地有一个排列。设通过点 $O$ 且与某两点连线垂直的所有直线的数目为 $k$ 。显见，$k\leqslant C_{8}^{2}\text{=}28$ 。由此产生
${{l}_{1}},{{l}_{2}},\cdots,{{l}_{2k}}$ 。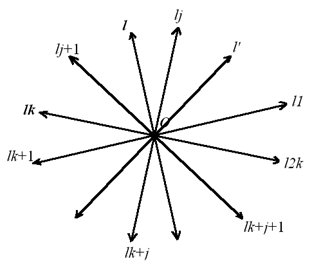如图，任意一条有向直线（不同于 ${{l}_{1}}\text{,}\cdots\text{,}{{l}_{2k}}$），一定存在两条相邻的有向直线 ${{l}_{j}}\text{,}{{l}_{j+1}}$，使得 ${{l}_{j}}\text{,}l\text{,}{{l}_{j+1}}$ 按逆时针方向排列。显见，对取定的 $j$，由这样的 $l$ 所得到的相应排列必相同。 若对不同于 ${{l}_{1}}\text{,}\cdots\text{,}{{l}_{2k}}$ 的两条有向直线 $l\text{,}{l}'$，不存在 $j$，使得 ${{l}_{j}}\text{,}l\text{,}{{l}_{j+1}}$ 及 ${{l}_{j}}\text{,}{l}'\text{,}{{l}_{j+1}}$ 都满足上一段叙述中所说的要求，则必有 $j$，使 ${l}',{{l}_{j}},l$ 按逆时针方向排列。设 ${{l}_{j}}$ 垂直于 ${{A}_{{{j}_{1}}}},{{A}_{{{j}_{2}}}}$ 在有向直线 $l\text{,}{l}'$ 上的射影次序一定不同，相应得到的排列必不同。 如上所述，不同的排列数为 $\text{2}k$ 。注意到，$k=C_{8}^{2}$ 是可以取到的，所以 ${{N}_{\text{8}}}\text{=56}$
答案 解析 备注
0.110973s