已知 $D$ 是 $\Delta ABC$ 的边 $AB$ 上的任意一点，$E$ 是边 $AC$ 上的任意一点，连结 $DE$，$F$ 是线段 $DE$ 上的任意一点。设 $\frac{AD}{AB}=x\text{,}\frac{AE}{AC}=y\text{,}\frac{DF}{DE}=z$ 。证明：（1）$S\Delta BCF\text{=}\left( 1-x \right)yzS\Delta ABC$，$S\Delta CEF=x\left( 1-y \right)\left( 1-z \right)S\Delta ABC$；（2）$\sqrt[3]{S\Delta BDF}+\sqrt[3]{S\Delta CEF}\leqslant \sqrt[3]{S\Delta ABC}$
【难度】
【出处】
2003第2届CGMO试题
【标注】
【答案】
略
【解析】
（1）如图，有 $S\Delta BDF=zS\Delta BDE\text{=}z\left( 1-x \right)S\Delta ABE\text{=}z\left( 1-x \right)yS\Delta ABC$，$S\Delta CEF=\left( 1-z \right)S\Delta CDE\text{=}\left( 1-z \right)\left(1-y \right)S\Delta ACD\text{=}\left( 1-z \right)\left( 1-y \right)x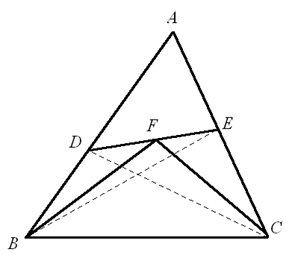S\Delta ABC$ 。 
（2）由（1）$\sqrt[3]{S\Delta BDF}+\sqrt[3]{S\Delta CEF}=\left( \sqrt[3]{\left(1-x \right)yz}+\sqrt[3]{x\left( 1-y \right)\left( 1-z \right)}\right)\sqrt[3]{S\Delta ABC}\leqslant \left( \frac{\left( 1-x\right)+y+z}{3}+\frac{x+\left( 1-y \right)+\left( 1-z \right)}{3}\right)\sqrt[3]{S\Delta ABC}=\sqrt[3]{S\Delta ABC}$
（2）由（1）$\sqrt[3]{S\Delta BDF}+\sqrt[3]{S\Delta CEF}=\left( \sqrt[3]{\left(1-x \right)yz}+\sqrt[3]{x\left( 1-y \right)\left( 1-z \right)}\right)\sqrt[3]{S\Delta ABC}\leqslant \left( \frac{\left( 1-x\right)+y+z}{3}+\frac{x+\left( 1-y \right)+\left( 1-z \right)}{3}\right)\sqrt[3]{S\Delta ABC}=\sqrt[3]{S\Delta ABC}$
答案
解析
备注
