如图,$ABCD$ 是圆内接四边形,$AC$ 是圆的直径,$BD\bot AC$,$AC$ 与 $BD$ 的交点为 $E$,$F$ 在 $DA$ 的延长线上。连结 $BF$,$G$ 在 $BA$ 的延长线上,使得 $DG\parallel BF$,$H$ 在 $BF$ 的延长线,$CH\bot GF$ 上。证明:$B,E,F,H$ 四点共圆。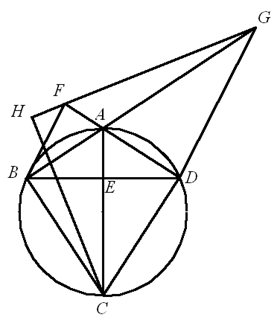

【难度】
【出处】
2003第2届CGMO试题
【标注】
【答案】
略
【解析】
连结 $BH,EF,CG$ 。因为 $\Delta BAF\text{ }\!\!\tilde{ }\!\!\text{ }\Delta GAD$(1),则 $\frac{FA}{AB}=\frac{DA}{AG}$ 。因为 $\Delta ABE\tilde{ }\Delta ACD$,则 $\frac{AB}{EA}=\frac{AC}{DA}$(2)。 $\left( 1\right)\times \left( 2 \right)$ 得 $\frac{FA}{EA}=\frac{AC}{AG}$ 。因为 $\angle FAE=\angle CAG$,所以 $\Delta FAE\tilde{ }\Delta CAG$ 。于是,$\angle FEA=\angle CGA$ 。由题设知,$\angle CBG=\angle CHG={{90}^{{}^\circ }}$,从而 $B,C,G,H$ 四点共圆。故 $\angle BHC=\angle BGC$ 。于是 $\angle BHF+\angle BEF=\angle BHC+{{90}^{{}^\circ }}+\angle BEF=\angle BGC+{{90}^{{}^\circ }}+\angle BEF=\angle FEA+{{90}^{{}^\circ }}+\angle BEF={{180}^{{}^\circ }}$ 所以 $B,E,F,H$ 四点共圆。
答案
解析
备注