设 $\Delta ABC$ 的三边长分别为 $AB=c\text{,}BC=a\text{,}CA\text{=}b$,$a\text{,}b\text{,}c$ 互不相等,$AD,BE,CF$ 分别为 $\Delta ABC$ 的三条内角分线,且 $DE=DF$ 。证明:(1)$\frac{a}{b+c}\text{=}\frac{b}{c+a}+\frac{c}{a+b}$;(2)$\angle BAC\text{}{{90}^{{}^\circ }}$
【难度】
【出处】
2003第2届CGMO试题
【标注】
【答案】
略
【解析】
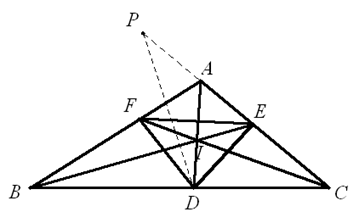 (1)如图,由正弦定理 $\frac{\sin \angle AFD}{\sin \angle FAD}\text{=}\frac{AD}{FD}=\frac{AD}{ED}=\frac{\sin \angle AED}{\sin \angle DAE}$ 。则 $\sin \angle AFD=\sin \angle AED$ 。故 $\angle AFD=\angle AED$ 或 $\angle AFD+\angle AED={{180}^{{}^\circ }}$ 。 若 $\angle AFD=\angle AED$,则 $\Delta AFD\cong \Delta AIE,AF=AE$ 。于是 $\Delta AIF\cong \Delta AIE,\angle AFI=\angle AEI$ 。从而 $\Delta AFC\cong \Delta AEB$,故 $AC=AB$,矛盾。所以 $\angle AFD+\angle AED={{180}^{{}^\circ }}$,$A,F,D,E$ 四点共圆。于是 $\angle DEC=\angle DFA>\angle ABC$ 。在 $CE$ 的延长线上取一点 $P$,使得 $\angle DPC=\angle B$,则 $PC=PE=CE$(1)。由 $\angle BFD=\angle PED,FD=ED$,得 $\Delta BFD\cong \Delta PED$ 。故 $PE=BF=\frac{ac}{a+b}$ 。 $\Delta PCD\cong \Delta BCA$,则 $\frac{PC}{BC}=\frac{CD}{CA}$ 。于是 $PC=a\cdot\frac{ba}{b+c}\cdot \frac{1}{b}=\frac{{{a}^{2}}}{b+c}$(2)。由(1)(2)得 $\frac{{{a}^{2}}}{b+c}\text{=}\frac{ac}{a+b}+\frac{ab}{c+a}$ 。所以,$\frac{a}{b+c}\text{=}\frac{b}{c+a}+\frac{c}{a+b}$ 。
(1)如图,由正弦定理 $\frac{\sin \angle AFD}{\sin \angle FAD}\text{=}\frac{AD}{FD}=\frac{AD}{ED}=\frac{\sin \angle AED}{\sin \angle DAE}$ 。则 $\sin \angle AFD=\sin \angle AED$ 。故 $\angle AFD=\angle AED$ 或 $\angle AFD+\angle AED={{180}^{{}^\circ }}$ 。 若 $\angle AFD=\angle AED$,则 $\Delta AFD\cong \Delta AIE,AF=AE$ 。于是 $\Delta AIF\cong \Delta AIE,\angle AFI=\angle AEI$ 。从而 $\Delta AFC\cong \Delta AEB$,故 $AC=AB$,矛盾。所以 $\angle AFD+\angle AED={{180}^{{}^\circ }}$,$A,F,D,E$ 四点共圆。于是 $\angle DEC=\angle DFA>\angle ABC$ 。在 $CE$ 的延长线上取一点 $P$,使得 $\angle DPC=\angle B$,则 $PC=PE=CE$(1)。由 $\angle BFD=\angle PED,FD=ED$,得 $\Delta BFD\cong \Delta PED$ 。故 $PE=BF=\frac{ac}{a+b}$ 。 $\Delta PCD\cong \Delta BCA$,则 $\frac{PC}{BC}=\frac{CD}{CA}$ 。于是 $PC=a\cdot\frac{ba}{b+c}\cdot \frac{1}{b}=\frac{{{a}^{2}}}{b+c}$(2)。由(1)(2)得 $\frac{{{a}^{2}}}{b+c}\text{=}\frac{ac}{a+b}+\frac{ab}{c+a}$ 。所以,$\frac{a}{b+c}\text{=}\frac{b}{c+a}+\frac{c}{a+b}$ 。(2)由(1)的结论有 $a\left( a+b \right)\left( a+c \right)\text{=}b\left(b+a \right)\left( b+c \right)+c\left( c+a \right)\left( c+b \right)$,${{a}^{2}}\left( a+b+c \right)\text{=}{{b}^{2}}\left(a+b+c \right)+{{c}^{2}}\left( a+b+c \right)+abc\text{}{{b}^{2}}\left( a+b+c\right)+{{c}^{2}}\left( a+b+c \right)$ 。由 ${{a}^{2}}\text{}{{b}^{2}}+{{c}^{2}}$ 。所以,$\angle BAC\text{}{{90}^{{}^\circ }}$ 。
答案
解析
备注