锐角 $\Delta ABC$ 的三条高分别为 $AD,BE,CF$ 。求证：$\Delta DEF$ 的周长不超过 $\Delta ABC$ 周长的一半。
【难度】
【出处】
2002第1届CGMO试题
【标注】
【答案】
略
【解析】
证法一：由于 $D,E,A,B$ 四点共圆，且 $AB$ 为该圆直径，根据正弦定理，可得 $\frac{DE}{\sin\angle DAE}\text{=}AB=c$，即 $DE=c\sin \angle DAE$ 。又 $\angle DCA={{90}^{{}^\circ }}-\angle DAC$，所以 $DE=c\cos C$ 。同理 $DF\text{=}b\cos B$ 。于是 $DE+DF\text{=}c\cos C+b\cos B\text{=}\left( 2R\operatorname{sinC} \right)\cos C+\left( 2R\sin B\right)\cos B=R\left( \sin 2C+\sin 2B \right)\text{=}2R\sin \left( B+C\right)\cos \left( B-C \right)\text{=}2R\sin A\cos \left( B-C \right)\text{=}a\cos\left( B-C \right)\leqslant a$ 。同理 $DE+EF\leqslant b\text{,}EF+DF\leqslant c$ 。将上述三式相加得 $DE+EF+FD\leqslant\frac{1}{2}\left( a+b+c \right)$ 证法二：设 $M$ 为 $BC$ 中点。 ${E}'$ 为 $E$ 关于 $BC$ 的对称点，$H$ 为 $\Delta ABC$ 的垂心。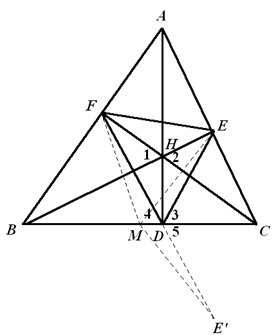 
如图，因 $B,D,H,F$ 四点共圆，故 $\angle 1=\angle4$ 。同理，$\angle 2=\angle 3$ 。又 $\angle 1=\angle 2$，故 $\angle 4=\angle 3$ 。又 $\angle 3=\angle 5$，所以 $\angle4=\angle 5$，$F,D,{E}'$ 三点共线。在直角 $\Delta BCE$ 和直角 $\Delta BCF$ 中，有 $EM=FM=\frac{1}{2}BC$ 。而 $M{E}'=ME$，故 $DE+DF=D{E}'+DF={E}'F\leqslant MF+M{E}'=BC$ 。同理，$DE+EF\leqslant AC,EF+FM\leqslant AB$ 。三式相加即知命题成立。
证法三：先证 $\Delta DEF$ 是锐角 $\Delta ABC$ 的所有内接三角形中周长最短的三角形。设点 ${D}'$ 是 $BC$ 边上任一固定点。如图，作点 ${D}'$ 关于 $AB,AC$ 的对称点，连结 ${{D}_{1}}{{D}_{2}}$ 分别交 $AB,AC$ 于点 ${E}',{F}'$，则 $\Delta{D}'{E}'{F}'$ 周长最短
。
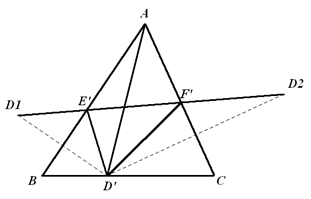事实上，$\Delta D{E}'{F}'$ 的周长 $={D}'{E}'+{E}'{F}'+{F}'{D}'={{D}_{1}}{E}'+{E}'{F}'+{F}'{{D}_{2}}={{D}_{1}}{{D}_{2}}$ 。在 $AB,AC$ 上任取 ${{E}_{1}},{{F}_{1}}$，则 $\Delta D{{E}_{1}}{{F}_{1}}$ 的周长 $=D{{E}_{1}}+{{E}_{1}}{{F}_{1}}+{{F}_{1}}D={{D}_{1}}{{E}_{1}}+{{E}_{1}}{{F}_{1}}+{{F}_{1}}{{D}_{2}}\geqslant{{D}_{1}}{{D}_{2}}$ 当且仅当 ${{E}_{1}},{{F}_{1}}$ 分别与 ${E}',{F}'$ 重合时取等号。所以，当点 ${D}'$ 固定时，上述 $\Delta{D}'{E}'{F}'$ 周长最短。因 $\angle {{D}_{1}}A{{D}_{2}}=2\angle BAC,A{{D}_{1}}={A}'D=A{{D}_{2}}$，根据余弦定理，${{D}_{1}}{{D}_{2}}$ 的长度仅与 $A{D}'$ 有关，当 $A{D}'$ 取最小值时，${{D}_{1}}{{D}_{2}}$ 也取最小值。此时，$\Delta {D}'{E}'{F}'$ 为中周长最短的内接三角形，故点 ${D}'$ 应为 $BC$ 边上高线的垂足 $D$ 。如图，$\Delta DEF$ 为 $\Delta ABC$ 的垂足三角形，则 $\Delta ABC$ 的三条高平分 $\Delta DEF$ 的内角，有 $\angle AFE=\angle DFC=\angle CF{{D}_{2}}$，从而 $E,F,{{D}_{2}}$ 三点共线。同理 ${{D}_{1}},E,F$ 三点共线。综上所述，垂足 $\Delta DEF$ 为 $\Delta ABC$ 中周长最短的内接三角形。分别在 $\Delta ABC$ 的三边上取中点 $M,N,L$，则 $DE+EF+FD\leqslant MN+NL+LM=\frac{1}{2}\left( AB+BC+CA \right)$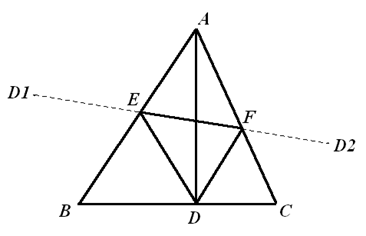
如图，因 $B,D,H,F$ 四点共圆，故 $\angle 1=\angle4$ 。同理，$\angle 2=\angle 3$ 。又 $\angle 1=\angle 2$，故 $\angle 4=\angle 3$ 。又 $\angle 3=\angle 5$，所以 $\angle4=\angle 5$，$F,D,{E}'$ 三点共线。在直角 $\Delta BCE$ 和直角 $\Delta BCF$ 中，有 $EM=FM=\frac{1}{2}BC$ 。而 $M{E}'=ME$，故 $DE+DF=D{E}'+DF={E}'F\leqslant MF+M{E}'=BC$ 。同理，$DE+EF\leqslant AC,EF+FM\leqslant AB$ 。三式相加即知命题成立。证法三：先证 $\Delta DEF$ 是锐角 $\Delta ABC$ 的所有内接三角形中周长最短的三角形。设点 ${D}'$ 是 $BC$ 边上任一固定点。如图，作点 ${D}'$ 关于 $AB,AC$ 的对称点，连结 ${{D}_{1}}{{D}_{2}}$ 分别交 $AB,AC$ 于点 ${E}',{F}'$，则 $\Delta{D}'{E}'{F}'$ 周长最短
。
事实上，$\Delta D{E}'{F}'$ 的周长 $={D}'{E}'+{E}'{F}'+{F}'{D}'={{D}_{1}}{E}'+{E}'{F}'+{F}'{{D}_{2}}={{D}_{1}}{{D}_{2}}$ 。在 $AB,AC$ 上任取 ${{E}_{1}},{{F}_{1}}$，则 $\Delta D{{E}_{1}}{{F}_{1}}$ 的周长 $=D{{E}_{1}}+{{E}_{1}}{{F}_{1}}+{{F}_{1}}D={{D}_{1}}{{E}_{1}}+{{E}_{1}}{{F}_{1}}+{{F}_{1}}{{D}_{2}}\geqslant{{D}_{1}}{{D}_{2}}$ 当且仅当 ${{E}_{1}},{{F}_{1}}$ 分别与 ${E}',{F}'$ 重合时取等号。所以，当点 ${D}'$ 固定时，上述 $\Delta{D}'{E}'{F}'$ 周长最短。因 $\angle {{D}_{1}}A{{D}_{2}}=2\angle BAC,A{{D}_{1}}={A}'D=A{{D}_{2}}$，根据余弦定理，${{D}_{1}}{{D}_{2}}$ 的长度仅与 $A{D}'$ 有关，当 $A{D}'$ 取最小值时，${{D}_{1}}{{D}_{2}}$ 也取最小值。此时，$\Delta {D}'{E}'{F}'$ 为中周长最短的内接三角形，故点 ${D}'$ 应为 $BC$ 边上高线的垂足 $D$ 。如图，$\Delta DEF$ 为 $\Delta ABC$ 的垂足三角形，则 $\Delta ABC$ 的三条高平分 $\Delta DEF$ 的内角，有 $\angle AFE=\angle DFC=\angle CF{{D}_{2}}$，从而 $E,F,{{D}_{2}}$ 三点共线。同理 ${{D}_{1}},E,F$ 三点共线。综上所述，垂足 $\Delta DEF$ 为 $\Delta ABC$ 中周长最短的内接三角形。分别在 $\Delta ABC$ 的三边上取中点 $M,N,L$，则 $DE+EF+FD\leqslant MN+NL+LM=\frac{1}{2}\left( AB+BC+CA \right)$
答案
解析
备注
