已知钝角 $\Delta ABC$ 的外接圆半径为 $1$ 。证明：存在一个斜边长为 $\sqrt{2}+1$ 的等腰直角三角形覆盖 $\Delta ABC$ 。
【难度】
【出处】
2004第3届CGMO试题
【标注】
【答案】
略
【解析】
不妨设 $\angle C\text{}{{90}^{{}^\circ }}$，于是 $\min\left\{ \angle A\text{,}\angle B \right\}\text{}{{45}^{{}^\circ }}$ 。不妨设 $\angle A\text{}{{45}^{{}^\circ }}$ 。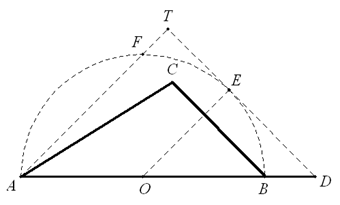
如图，以 $AB$ 为直径，在顶点 $C$ 的同侧作半圆 $\odot O$，则 $C$ 位于半圆内。作射线 $AT$ 使得 $\angle BAT\text{=}{{45}^{{}^\circ }}$，作射线 $OE$ 使得 $\angle BOE\text{=}{{45}^{{}^\circ }}$ 且与半圆交于点 $E$ 。过点 $E$ 作半圆的切线，分别交 $AB$ 的延长线 $AT$ 和于点 $D$ 和点 $F$ 。则等腰直角 $\Delta ADF$ 覆盖 $\Delta ABC$，且 $AD=AO+OD=\frac{1}{2}AB+\sqrt{2}\cdot\frac{1}{2}AB=\frac{1}{2}\left( 1+\sqrt{2} \right)\cdot 2R=1+\sqrt{2}$
如图，以 $AB$ 为直径，在顶点 $C$ 的同侧作半圆 $\odot O$，则 $C$ 位于半圆内。作射线 $AT$ 使得 $\angle BAT\text{=}{{45}^{{}^\circ }}$，作射线 $OE$ 使得 $\angle BOE\text{=}{{45}^{{}^\circ }}$ 且与半圆交于点 $E$ 。过点 $E$ 作半圆的切线，分别交 $AB$ 的延长线 $AT$ 和于点 $D$ 和点 $F$ 。则等腰直角 $\Delta ADF$ 覆盖 $\Delta ABC$，且 $AD=AO+OD=\frac{1}{2}AB+\sqrt{2}\cdot\frac{1}{2}AB=\frac{1}{2}\left( 1+\sqrt{2} \right)\cdot 2R=1+\sqrt{2}$
答案
解析
备注
