给定锐角 $\Delta ABC$，点 $O$ 为其外心，直线 $AO$ 交边 $BC$ 于点 $D$ 。动点 $E,F$ 分别位于边 $AB,AC$ 上，使得 $A,E,D,F$ 四点共圆。求证：线段 $EF$ 在边 $BC$ 上的投影长度为定值。
【难度】
【出处】
2004第3届CGMO试题
【标注】
【答案】
略
【解析】
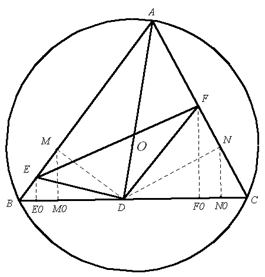如图，设 $EF$ 在边 $BC$ 上的投影为 ${{E}_{0}}{{F}_{0}}$，过点 $D$ 分别作 $DM\bot AB$ 于 $M$，$DN\bot AC$ 于 $N$，过点 $M,N$ 分别作 $M{{M}_{0}}\bot BC$ 于 ${{M}_{0}}$ 和 $N{{N}_{0}}\bot BC$ 于 ${{N}_{0}}$ 。由 $\angle AMD=\angle AND={{90}^{{}^\circ }}$，知 $\angle MDN={{180}^{{}^\circ }}-\angle BAC$ 。 因为 $\angle EDF={{180}^{{}^\circ }}-\angle BAC$，所以 $\angle MDE=\angle NDF$ 。 因此 $Rt\Delta DME\sim Rt\Delta DNF$，故 $\frac{EM}{FN}=\frac{DM}{DN}=\frac{AD\sin \angle DAM}{AD\sin \angle DAN}=\frac{\sin \angle DAM}{\sin \angle DAN}$ 。 又 $\angle OAB\text{=}\frac{1}{2}\left( {{180}^{{}^\circ }}-2\angle C\right)\text{=}{{90}^{{}^\circ }}-\angle C$，$\angle OAC\text{=}\frac{1}{2}\left( {{180}^{{}^\circ }}-2\angle B\right)\text{=}{{90}^{{}^\circ }}-\angle B$，则 $\frac{EM}{FN}=\frac{\cos C}{\cos B}$（1）。由平行线所截线段对应成比例知 $\frac{{{E}_{0}}{{M}_{0}}}{EM}=\frac{B{{M}_{0}}}{BM}=\cos B$，$\frac{{{F}_{0}}{{N}_{0}}}{FN}=\frac{C{{N}_{0}}}{CN}=\cos C$ 。故 $\frac{\cos B}{\cos C}=\frac{{{E}_{0}}{{M}_{0}}}{{{F}_{0}}{{N}_{0}}}.\frac{FN}{EM}$（2）。由（1）（2）得 ${{E}_{0}}{{M}_{0}}={{F}_{0}}{{N}_{0}}$，故 ${{E}_{0}}{{F}_{0}}={{M}_{0}}{{N}_{0}}$（定值）
答案
解析
备注
