如图,点 $P$ 在 $\Delta ABC$ 的外接圆上,直线 $CP,AB$ 相交于点 $E$,直线 $BP,AC$ 相交于点 $F$,边 $AC$ 的垂直平分线交边 $AB$ 于点 $J$,边 $AB$ 的垂直平分线交边 $AC$ 于点 $K$ 。求证:$\frac{C{{E}^{2}}}{B{{F}^{2}}}=\frac{AJ\cdot JE}{AK\cdot KF}$ 。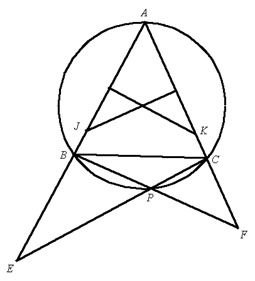

【难度】
【出处】
2005第4届CGMO试题
【标注】
【答案】
略
【解析】
如图,联结 $BKCJ$,则 $\angle E=\angle ABP-\angle BPE$ 。由 $A$、$B$、$P$、$C$ 四点共圆,知 $\angle BPE\text{=}\angle A$,故 $\angle E=\angle ABP-\angle A$ 。又 $KA=KB$,知 $\angle A=\angle ABK$ 。 所以有 $\angle E=\angle ABP-\angle ABK=\angle KBF$ 。(1)同理,$\angle F=\angle JCE$ 。(2)由(1),(2)得 $\Delta JEC\sim \Delta KBF$,有 $\frac{CE}{BF}=\frac{JE}{KB}=\frac{JE}{AK}$,$\frac{CE}{BF}=\frac{JC}{KF}=\frac{AJ}{KF}$ 。 将以上两式左、右两端分别相乘即得结论。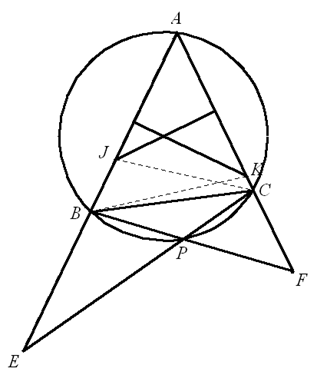

答案
解析
备注