设凸四边形 $ABCD$ 的对角线交于点 $O$ 。 $\Delta OAD$ 和 $\Delta OBC$ 的外接圆交于点 $O$ 和 $M$，直线 $OM$ 分别交 $\Delta OAB$ 和 $\Delta OCD$ 的外接圆于点 $T$ 和 $S$ 。求证：$M$ 是线段 $TS$ 的中点。
【难度】
【出处】
2006第5届CGMO试题
【标注】
【答案】
略
【解析】
证法1：如图，联结 $BT$、$CS$、$MA$、$MB$、$MC$、$MD$ 。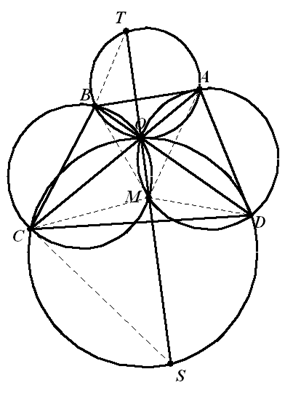
因为 $\angle BTO=\angle BAO$，$\angle BCO=\angle BMO$，所以 $\Delta BTM\sim \Delta BAC$，得 $\frac{TM}{AC}=\frac{BM}{BC}$ 。（1）同理，$\Delta CMS\sim\Delta CBD$，得 $\frac{MS}{BD}=\frac{CM}{BC}$ 。（2）（1）（2）相除得到 $\frac{TM}{MS}=\frac{BM}{CM}\cdot \frac{AC}{BD}$ 。（3）又 $\angle MBD=\angle MCA$，$\angle MDB=\angle MAC$，所以 $\Delta MBD\sim\Delta MCA$，得 $\frac{BM}{CM}=\frac{BD}{AC}$ 。（4）将（4）式带入（3）式，得到 $TM=MS$ 。 证法2：如图，设 $\Delta OAB$、$\Delta OBC$、$\Delta OCD$、$\Delta ODA$ 的外心分别为 ${{O}_{1}}$、${{O}_{2}}$、${{O}_{3}}$、${{O}_{4}}$，过点 ${{O}_{1}}$、${{O}_{3}}$ 作 $TS$ 的垂线，垂足分别为 $E$、$F$ 。联结 ${{O}_{2}}{{O}_{4}}$ 交 $TS$ 于点 $G$ 。
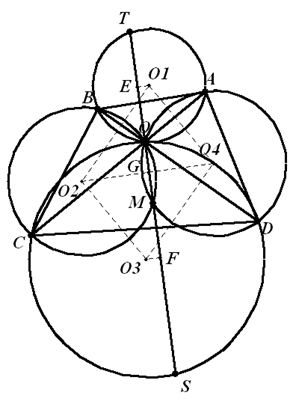因 $OM$ 是 $\odot {{O}_{2}}$、$\odot{{O}_{4}}$ 的公共弦，故 ${{O}_{2}}{{O}_{4}}$ 垂直平分 $OM$，即 $G$ 是线段 $OM$ 的中点。同样，${{O}_{1}}{{O}_{4}}$ 垂直平分 $OA$，${{O}_{2}}{{O}_{3}}$ 垂直平分 $OC$，得 ${{O}_{1}}{{O}_{4}}\parallel {{O}_{2}}{{O}_{3}}$ 。同理，${{O}_{1}}{{O}_{2}}\parallel {{O}_{3}}{{O}_{4}}$ 。因此，四边形 ${{O}_{1}}{{O}_{2}}{{O}_{3}}{{O}_{4}}$ 是平行四边形，其对角线互相平分。易知，$EG=FG$ 。又由垂径定理，知 $E$ 是 $TO$ 中点，$F$ 是 $OS$ 中点。 因此，$TM=TO+OM=2EO+2OG=2EG$，$MS=OS-OM=2OF-2OG=2GF$ 。所以 $TM=MS$ 。
因为 $\angle BTO=\angle BAO$，$\angle BCO=\angle BMO$，所以 $\Delta BTM\sim \Delta BAC$，得 $\frac{TM}{AC}=\frac{BM}{BC}$ 。（1）同理，$\Delta CMS\sim\Delta CBD$，得 $\frac{MS}{BD}=\frac{CM}{BC}$ 。（2）（1）（2）相除得到 $\frac{TM}{MS}=\frac{BM}{CM}\cdot \frac{AC}{BD}$ 。（3）又 $\angle MBD=\angle MCA$，$\angle MDB=\angle MAC$，所以 $\Delta MBD\sim\Delta MCA$，得 $\frac{BM}{CM}=\frac{BD}{AC}$ 。（4）将（4）式带入（3）式，得到 $TM=MS$ 。 证法2：如图，设 $\Delta OAB$、$\Delta OBC$、$\Delta OCD$、$\Delta ODA$ 的外心分别为 ${{O}_{1}}$、${{O}_{2}}$、${{O}_{3}}$、${{O}_{4}}$，过点 ${{O}_{1}}$、${{O}_{3}}$ 作 $TS$ 的垂线，垂足分别为 $E$、$F$ 。联结 ${{O}_{2}}{{O}_{4}}$ 交 $TS$ 于点 $G$ 。因 $OM$ 是 $\odot {{O}_{2}}$、$\odot{{O}_{4}}$ 的公共弦，故 ${{O}_{2}}{{O}_{4}}$ 垂直平分 $OM$，即 $G$ 是线段 $OM$ 的中点。同样，${{O}_{1}}{{O}_{4}}$ 垂直平分 $OA$，${{O}_{2}}{{O}_{3}}$ 垂直平分 $OC$，得 ${{O}_{1}}{{O}_{4}}\parallel {{O}_{2}}{{O}_{3}}$ 。同理，${{O}_{1}}{{O}_{2}}\parallel {{O}_{3}}{{O}_{4}}$ 。因此，四边形 ${{O}_{1}}{{O}_{2}}{{O}_{3}}{{O}_{4}}$ 是平行四边形，其对角线互相平分。易知，$EG=FG$ 。又由垂径定理，知 $E$ 是 $TO$ 中点，$F$ 是 $OS$ 中点。 因此，$TM=TO+OM=2EO+2OG=2EG$，$MS=OS-OM=2OF-2OG=2GF$ 。所以 $TM=MS$ 。
答案
解析
备注
