2007第6届CGMO试题

• 知识点

  >

  二试几何部分

略

从六个比值中取出两个，共有两种类型：（1）涉及同一边；（2）涉及不同边。（1）如果同一边上的两个比值同时是整数，不妨设为 $\frac{BD}{DC}$、$\frac{CD}{DB}$ 。因它们互为倒数，又同是整数，所以必须都取 $1$，则 $BD=DC$ 。由于 $O$ 是 $\Delta ABC$ 的外心，进而得 $AD$ 是边 $BC$ 的中垂线。于是，$AB=AC$ 。（2）记 $\angle CAB=\alpha $，$\angle ABC\text{=}\beta $，$\angle BCA\text{=}\gamma $ 。因为 $\Delta ABC$ 是锐角三角形，所以，$\angle BOC\text{=}2\alpha $，$\angle COA\text{=}2\beta $，$\angle AOB\text{=}2\gamma $ 。于是，$\frac{BD}{DC}\text{=}\frac{S\Delta OAB}{S\Delta OAC}\text{=}\frac{\sin 2\gamma }{\sin 2\beta }$ 。同理，$\frac{CE}{EA}\text{=}\frac{\sin2\alpha }{\sin 2\gamma }$，$\frac{AF}{FB}=\frac{\sin 2\beta }{\sin 2\alpha }$ 。若上述六个比值中有两个同时是整数且涉及不同的边时，则存在整数 $m$、$n$，使得 $\sin2x=m\sin 2z$ 且 $\sin 2y\text{=}n\sin 2z$（1）或 $\sin2z\text{=}m\sin 2x$ 且 $\sin 2z\text{=}n\sin 2y$（2），其中，$x$、$y$、$z$ 是 $\alpha $、$\beta $、$\gamma $ 的某种排列。 以下构造 $\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}$，使得它的三个内角分别为 ${{180}^{{}^\circ }}-2\alpha $，${{180}^{{}^\circ}}-2\beta $，${{180}^{{}^\circ }}-2\gamma $ 。如图，过点 $A$、$B$、$C$ 分别作 $\Delta ABC$ 外接圆的切线，所围成的 $\Delta{{A}_{1}}{{B}_{1}}{{C}_{1}}$ 即满足要求。 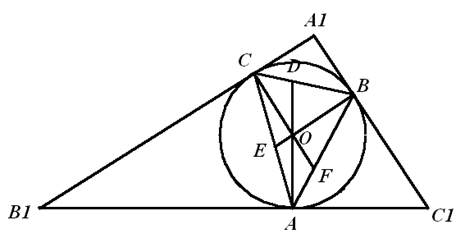 根据正弦定理，知 $\Delta{{A}_{1}}{{B}_{1}}{{C}_{1}}$ 的三边与 $\sin 2\alpha $、$\sin 2\beta $、$\sin 2\gamma $ 成正比。在式（1）（2）两种情况下，可知其三边之比分别为 $1:m:n$ 或 $m:n:mn$ 。对于式（1），由三角形两边之和大于第三边，可知必须 $m\text{=}n$；对于式（2），要保证 $m+n$ > $mn$．，即 $\left( m-1 \right)\left( n-1 \right)$ < $1$，由此，$m$、$n$ 中必有一个为 $1$ 。无论哪种情况，都有 $\Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}$ 是等腰三角形。因此，$\Delta ABC$ 是等腰三角形。