2007第6届CGMO试题

• 知识点

  >

  二试几何部分

略

（1）记 $S$ 中的 $n$ 个点为 ${{A}_{1}}\text{,}{{A}_{2}}\text{,}\cdots\text{,}{{A}_{n}}$ 。建立直角坐标系，设 ${{A}_{i}}\left( {{x}_{i}}\text{,}{{y}_{i}} \right)\left(i\text{=}1\text{,}2\text{,}\ddots \text{,}n \right)$ 。易证 $\displaystyle \sum\limits_{i\text{=}1}^{n}{B{{A}_{i}}\text{=}0\Leftrightarrow B\left(\frac{1}{n}\sum\limits_{i\text{=}1}^{n}{{{x}_{i}}}\text{,}\frac{1}{n}\sum\limits_{i\text{=}1}^{n}{{{y}_{i}}}\right)}$ 。这说明，平面内存在唯一的一点 $B$，使 $\displaystyle \sum\limits_{i\text{=}1}^{n}{B{{A}_{i}}}\text{=}0$ 。我们称 $B$ 为点集 $S$ 的“质心”。 如果任取 $P$ 中一条直线 $l$ 为 $x$ 轴，建立直角坐标系，则 $\displaystyle \sum\limits_{i\text{=}1}^{n}{{{y}_{i}}}\text{=}0$ 。 故点 $B$ 在 $l$ 上。即 $P$ 中每一条直线均过质心 $B$ 。（2）设 $F=\left\{\left. \left( X,Y,l \right) \right|X,Y\in S,l\in P,l\bot XY,ifM=XY\cap l,MX=MY\right\}$，${{F}_{1}}=\left\{ \left. \left(X,Y,l \right)\in F \right|X\ne Y \right\}$，${{F}_{2}}=\left\{ \left. \left( X,X,l \right)\in F \right|X\in l\right\}$ 。显然，$F={{F}_{1}}\bigcup {{F}_{2}}\text{,}{{F}_{1}}\bigcap {{F}_{2}}=\varnothing $ 。（1）考虑 $P$ 中任一直线 $l$，$X$ 为 $S$ 中任一点，$X$ 关于 $l$ 的对称点 $Y$ 是唯一的。即对每一个 $l$，三元有序组 $\left( X,Y,l \right)$ 有 $n$ 个，故 $\left|F \right|=mn$ 。（2）对于 ${{F}_{1}}$ 中的三元有序组 $\left(X,Y,l \right)$，因为不同的两点 $X$、$Y$ 的对称轴只有 $1$ 条，所以 $\left| {{F}_{1}} \right|\leqslant \left\{ \left. \left( X,Y \right)\right|X,Y\in S,X\ne Y \right\}=2C_{n}^{2}\text{=}n\left( n-1 \right)$（3）
1．当 $S$ 中任一点至多在 $P$ 中的一条直线 $l$ 上时，$\left| {{F}_{2}} \right|\leqslant \left\{ \left. X \right|X\in S\right\}=n$ 。（4）由（1）（2）（3）（4）得 $mn\leqslant n\left( n-1 \right)+n\Rightarrow m\leqslant n$ 。
2．当 $S$ 中存在一点同时在 $P$ 中的两条直线上时，由（1）中所证，此点即为质心 $B$ 。
综合1，2，得 $m\leqslant n$（3）当 $m\text{=}n$ 时，由（2）所证，式（3）（4）同时取等号，即 $S$ 中任意两点的中垂线均属于 $P$，$S$ 中每点恰好在 $P$ 中的一条直线上，同时质心 $B$ 不在 $S$ 中。 首先，指出 $B{{A}_{i}}\left(i\text{=}1\text{,}2\text{,}\cdots \text{,}n \right)$ 相等。否则，如果存在 $j\text{,}k\left(1\leqslant j\text{}k\leqslant n \right)$，使得 $B{{A}_{j}}\ne B{{A}_{k}}$，则线段 ${{A}_{j}}{{A}_{k}}$ 的对称轴不过点 $B$，与（1）所证矛盾。因此，${{A}_{1}}\text{,}{{A}_{2}}\text{,}\cdots \text{,}{{A}_{n}}$ 均在以点 $B$ 为圆心的圆上，记此圆为 $\odot B$ 。不妨设 ${{A}_{1}}\text{,}{{A}_{2}}\text{,}\cdots \text{,}{{A}_{n}}$ 按顺时针排列。 其次，${{A}_{1}}\text{,}{{A}_{2}}\text{,}\cdots\text{,}{{A}_{n}}$ 是 $\odot B$ 的 $n$ 个等分点。否则，如果存在 $i\left( 1\leqslant i\leqslant n \right)$，使 ${{A}_{i}}{{A}_{i+1}}\ne{{A}_{i+1}}{{A}_{i+2}}$（定义 ${{A}_{n+1}}={{A}_{1}}$，${{A}_{n+2}}={{A}_{2}}$）。不妨设 ${{A}_{i}}{{A}_{i+1}}$ < ${{A}_{i+1}}{{A}_{i+2}}$ 。如图，线段 ${{A}_{i}}{{A}_{i+2}}$ 的对称轴 ${l}'\in P$，而 ${{A}_{i+1}}$ 关于 ${l}'$ 的对称点在弧 ${{A}_{i+1}}{{A}_{i+2}}$ 上（不含端点）。这与 ${{A}_{i+1}}$、${{A}_{i+2}}$ 相邻矛盾。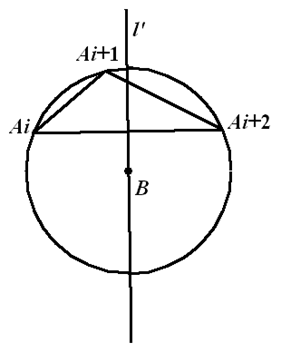 因此 $m\text{=}n$ 时，集 $S$ 中的点是正 $n$ 边形的 $n$ 个顶点。易知正 $n$ 边形有 $n$ 条对称轴。故当且仅当 $S$ 中的点组成正 $n$ 边形的 $n$ 个顶点，$P$ 是正 $n$ 边形的 $n$ 条对称轴时，$m\text{=}n$ 。