设 $D$ 是 $\Delta ABC$ 内的一点，满足 $\angle DAC\text{=}\angle DCA\text{=}{{30}^{{}^\circ }}$，$\angle DBA\text{=}{{60}^{{}^\circ }}$，$E$ 是边 $BC$ 的中点，$F$ 是边 $AC$ 的三等分点，满足 $AF=2FC$ 。求证：$DE\bot EF$ 。
【难度】
【出处】
2007第6届CGMO试题
【标注】
【答案】
略
【解析】
证法1：如图，作 $DM\bot AC$ 于点 $M$，$FN\bot CD$ 于点 $N$，联结 $EM$、$EN$ 。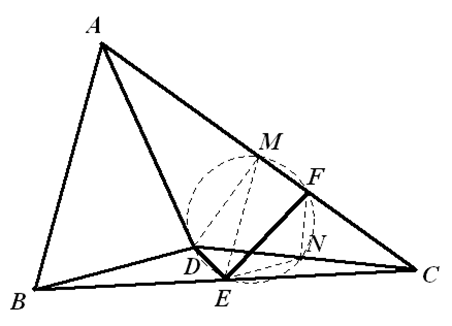
设 $CF=a$，$AF\text{=}2a$，则 $CN\text{=}CF\cos{{30}^{{}^\circ }}\text{=}\frac{\sqrt{3}a}{2}\text{=}\frac{1}{2}CD$，即 $N$ 是 $CD$ 的中点。又因为 $M$ 是边 $AC$ 上的中点，$E$ 是边 $BC$ 上的中点，所以，$EM\parallel AB$，$EN\parallel BD$，得 $\angle MEN=\angle ABD\text{=}{{60}^{{}^\circ }}\text{=}\angle MDC$ 。故 $M$、$D$、$E$、$N$ 四点共圆。又因为 $D$、$M$、$F$、$N$ 四点共圆，所以 $D$、$E$、$F$、$M$、$N$ 五点共圆。从而 $\angle DEF\text{=}{{90}^{{}^\circ }}$ 。 证法2：建立复平面，令 $B\text{=}0$，$D=1$，$A\text{=}-{{\omega }^{2}}k$ 。经计算可得 $C\text{=}1-{{\omega}^{2}}-\omega k$，$E\text{=}\frac{B+C}{2}=\frac{1-{{\omega }^{2}}-\omega k}{2}$，$F\text{=}\frac{2C+A}{3}\text{=}\frac{2-2{{\omega }^{2}}-2\omega k-{{\omega}^{2}}k}{3}$ 。于是，$E-1\text{=}-\frac{1+{{\omega }^{2}}+\omega k}{2}$，$F-E=\frac{1-{{\omega}^{2}}-\left( \omega +2{{\omega }^{2}} \right)k}{6}$ 。故 $\frac{F-E}{E-1}=\frac{1}{3}\cdot\frac{{{\omega }^{2}}-1+\left( \omega +2{{\omega }^{2}} \right)k}{1+{{\omega}^{2}}+\omega k}=\frac{\omega -{{\omega }^{2}}}{3}\cdot\frac{k+1}{k-1}=\frac{i}{\sqrt{3}}\cdot \frac{k+1}{k-1}$ 。 因此，$DE\bot EF$，即 $\angle DEF={{90}^{{}^\circ }}$ 。
设 $CF=a$，$AF\text{=}2a$，则 $CN\text{=}CF\cos{{30}^{{}^\circ }}\text{=}\frac{\sqrt{3}a}{2}\text{=}\frac{1}{2}CD$，即 $N$ 是 $CD$ 的中点。又因为 $M$ 是边 $AC$ 上的中点，$E$ 是边 $BC$ 上的中点，所以，$EM\parallel AB$，$EN\parallel BD$，得 $\angle MEN=\angle ABD\text{=}{{60}^{{}^\circ }}\text{=}\angle MDC$ 。故 $M$、$D$、$E$、$N$ 四点共圆。又因为 $D$、$M$、$F$、$N$ 四点共圆，所以 $D$、$E$、$F$、$M$、$N$ 五点共圆。从而 $\angle DEF\text{=}{{90}^{{}^\circ }}$ 。 证法2：建立复平面，令 $B\text{=}0$，$D=1$，$A\text{=}-{{\omega }^{2}}k$ 。经计算可得 $C\text{=}1-{{\omega}^{2}}-\omega k$，$E\text{=}\frac{B+C}{2}=\frac{1-{{\omega }^{2}}-\omega k}{2}$，$F\text{=}\frac{2C+A}{3}\text{=}\frac{2-2{{\omega }^{2}}-2\omega k-{{\omega}^{2}}k}{3}$ 。于是，$E-1\text{=}-\frac{1+{{\omega }^{2}}+\omega k}{2}$，$F-E=\frac{1-{{\omega}^{2}}-\left( \omega +2{{\omega }^{2}} \right)k}{6}$ 。故 $\frac{F-E}{E-1}=\frac{1}{3}\cdot\frac{{{\omega }^{2}}-1+\left( \omega +2{{\omega }^{2}} \right)k}{1+{{\omega}^{2}}+\omega k}=\frac{\omega -{{\omega }^{2}}}{3}\cdot\frac{k+1}{k-1}=\frac{i}{\sqrt{3}}\cdot \frac{k+1}{k-1}$ 。 因此，$DE\bot EF$，即 $\angle DEF={{90}^{{}^\circ }}$ 。
答案
解析
备注
