求最小常数 $a\left( a \right.$ > $\left. 1 \right)$，使得对正方形 $ABCD$ 内部任一点 $P$，都存在 $\Delta PAB$、$\Delta PBC$、$\Delta PCD$、$\Delta PDA$ 中的某两个三角形，其面积之比属于区间 $\left[ {{a}^{-1}}\text{,}a \right]$ 。
【难度】
【出处】
2008第7届CGMO试题
【标注】
【答案】
${{a}_{\min }}\text{=}\frac{1+\sqrt{5}}{2}$
【解析】
首先证明 ${{a}_{\min }}\leqslant \frac{1+\sqrt{5}}{2}$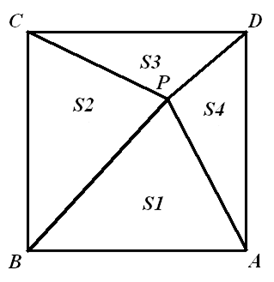 
记 $\varphi \text{=}\frac{1+\sqrt{5}}{2}$，不妨设正方形边长为 $\sqrt{2}$ 。如图，对正方形 $ABCD$ 内部一点 $P$，令 ${{S}_{1}}$、${{S}_{2}}$、${{S}_{3}}$、${{S}_{4}}$ 分别表示 $\Delta PAB$、$\Delta PBC$、$\Delta PCD$、$\Delta PDA$ 的面积。不妨设 ${{S}_{1}}\geqslant {{S}_{2}}\geqslant {{S}_{4}}\geqslant {{S}_{3}}$ 。令 $\lambda\text{=}\frac{{{S}_{1}}}{{{S}_{2}}}$，$\mu \text{=}\frac{{{S}_{2}}}{{{S}_{4}}}$ 。如果 $\lambda\text{,}\mu $ > $\varphi $，由 ${{S}_{1}}+{{S}_{3}}\text{=}{{S}_{2}}+{{S}_{4}}\text{=}1$，得 $\frac{{{S}_{2}}}{1-{{S}_{2}}}\text{=}\mu\Rightarrow {{S}_{2}}\text{=}\frac{\mu }{1+\mu }$ 。故 ${{S}_{1}}\text{=}\lambda{{S}_{2}}\text{=}\frac{\lambda \mu }{1+\mu }\text{=}\frac{\lambda}{1+\frac{1}{\mu }}$ > $\frac{\varphi }{1+\frac{1}{\varphi}}\text{=}\frac{{{\varphi }^{2}}}{1+\varphi }\text{=}1$，矛盾。 因此，$\min \left\{\lambda \text{,}\mu \right\}\leqslant \varphi$，这表明 ${{a}_{\min }}\leqslant \varphi $ 。 反过来，对于任意的 $a\in \left( 1\text{,}\varphi \right)$，取定 $t\in \left( a\text{,}\frac{1+\sqrt{5}}{2} \right)$，使得 $b\text{=}\frac{{{t}^{2}}}{1+t}$ > $\frac{8}{9}$ 。在正方形 $ABCD$ 内取一点 $P$，使得 ${{S}_{1}}\text{=}b$，${{S}_{2}}\text{=}\frac{b}{t}$，${{S}_{3}}\text{=}\frac{b}{{{t}^{2}}}$，${{S}_{4}}\text{=}1-b$ 。 则 $\frac{{{S}_{1}}}{{{S}_{2}}}=\frac{{{S}_{2}}}{{{S}_{3}}}=t\in\left( a\text{,}\frac{1+\sqrt{5}}{2} \right)$，$\frac{{{S}_{3}}}{{{S}_{4}}}\text{=}\frac{b}{{{t}^{2}}\left(1-b \right)}$ > $\frac{b}{4\left( 1-b \right)}$ > $2$ > $a$ 。由此得到对任意的 $i$、$j\in\left\{ 1\text{,}2\text{,}3\text{,}4 \right\}$，有 $\frac{{{S}_{i}}}{{{S}_{j}}}\notin\left[ {{a}^{-1}}\text{,}a \right]$ 。这表明 ${{a}_{\min }}\text{=}\varphi $ 。
记 $\varphi \text{=}\frac{1+\sqrt{5}}{2}$，不妨设正方形边长为 $\sqrt{2}$ 。如图，对正方形 $ABCD$ 内部一点 $P$，令 ${{S}_{1}}$、${{S}_{2}}$、${{S}_{3}}$、${{S}_{4}}$ 分别表示 $\Delta PAB$、$\Delta PBC$、$\Delta PCD$、$\Delta PDA$ 的面积。不妨设 ${{S}_{1}}\geqslant {{S}_{2}}\geqslant {{S}_{4}}\geqslant {{S}_{3}}$ 。令 $\lambda\text{=}\frac{{{S}_{1}}}{{{S}_{2}}}$，$\mu \text{=}\frac{{{S}_{2}}}{{{S}_{4}}}$ 。如果 $\lambda\text{,}\mu $ > $\varphi $，由 ${{S}_{1}}+{{S}_{3}}\text{=}{{S}_{2}}+{{S}_{4}}\text{=}1$，得 $\frac{{{S}_{2}}}{1-{{S}_{2}}}\text{=}\mu\Rightarrow {{S}_{2}}\text{=}\frac{\mu }{1+\mu }$ 。故 ${{S}_{1}}\text{=}\lambda{{S}_{2}}\text{=}\frac{\lambda \mu }{1+\mu }\text{=}\frac{\lambda}{1+\frac{1}{\mu }}$ > $\frac{\varphi }{1+\frac{1}{\varphi}}\text{=}\frac{{{\varphi }^{2}}}{1+\varphi }\text{=}1$，矛盾。 因此，$\min \left\{\lambda \text{,}\mu \right\}\leqslant \varphi$，这表明 ${{a}_{\min }}\leqslant \varphi $ 。 反过来，对于任意的 $a\in \left( 1\text{,}\varphi \right)$，取定 $t\in \left( a\text{,}\frac{1+\sqrt{5}}{2} \right)$，使得 $b\text{=}\frac{{{t}^{2}}}{1+t}$ > $\frac{8}{9}$ 。在正方形 $ABCD$ 内取一点 $P$，使得 ${{S}_{1}}\text{=}b$，${{S}_{2}}\text{=}\frac{b}{t}$，${{S}_{3}}\text{=}\frac{b}{{{t}^{2}}}$，${{S}_{4}}\text{=}1-b$ 。 则 $\frac{{{S}_{1}}}{{{S}_{2}}}=\frac{{{S}_{2}}}{{{S}_{3}}}=t\in\left( a\text{,}\frac{1+\sqrt{5}}{2} \right)$，$\frac{{{S}_{3}}}{{{S}_{4}}}\text{=}\frac{b}{{{t}^{2}}\left(1-b \right)}$ > $\frac{b}{4\left( 1-b \right)}$ > $2$ > $a$ 。由此得到对任意的 $i$、$j\in\left\{ 1\text{,}2\text{,}3\text{,}4 \right\}$，有 $\frac{{{S}_{i}}}{{{S}_{j}}}\notin\left[ {{a}^{-1}}\text{,}a \right]$ 。这表明 ${{a}_{\min }}\text{=}\varphi $ 。
答案
解析
备注
