在凸四边形 $ABCD$ 的外部分别作正 $\Delta ABQ$、$\Delta BCR$、$\Delta CDS$、$\Delta DAP$ 。记四边形 $ABCD$ 的对角线的和为 $x$，四边形 $PQRS$ 的对边中点连线的和为 $y$ 。求 $\frac{y}{x}$ 的最大值。
【难度】
【出处】
2008第7届CGMO试题
【标注】
【答案】
$\frac{1+\sqrt{3}}{2}$
【解析】
当四边形 $ABCD$ 是正方形时，得 $\frac{y}{x}\text{=}\frac{1+\sqrt{3}}{2}$ 。下面证明 $\frac{y}{x}\leqslant\frac{1+\sqrt{3}}{2}$：如图，设 ${{P}_{1}}$、${{Q}_{1}}$、${{R}_{1}}$、${{S}_{1}}$ 分别是边 $DA$、$AB$、$BC$、$CD$ 的中点，$SP$、$PQ$、$QR$、$RS$ 的中点分别为 $E$、$F$、$G$、$H$ 。则四边形 ${{P}_{1}}{{Q}_{1}}{{R}_{1}}{{S}_{1}}$ 是平行四边形。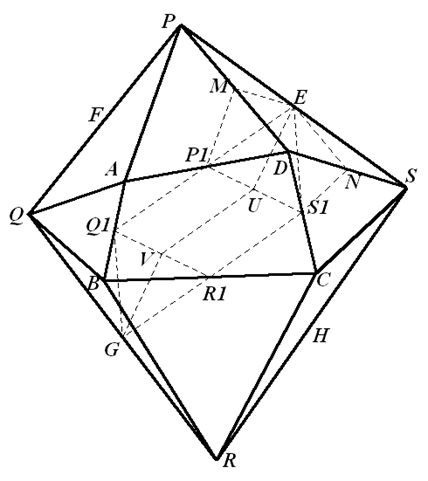
联结 ${{P}_{1}}E$、${{S}_{1}}E$ 。设 $M$、$N$ 分别是 $DP$、$DS$ 的中点。则 $D{{S}_{1}}={{S}_{1}}N=DN=EM$，$D{{P}_{1}}={{P}_{1}}M=MD=EN$ 。又 $\angle {{P}_{1}}D{{S}_{1}}={{360}^{{}^\circ}}-{{60}^{{}^\circ }}-{{60}^{{}^\circ }}-\angle PDS={{240}^{{}^\circ }}-\left({{180}^{{}^\circ }}-\angle END \right)={{60}^{{}^\circ }}+\angle END=\angle EN{{S}_{1}}=\angle EM{{P}_{1}}$ 则 $\Delta D{{P}_{1}}{{S}_{1}}\cong \Delta M{{P}_{1}}E\cong \Delta NE{{S}_{1}}$，从而 $\Delta E{{P}_{1}}{{S}_{1}}$ 是正三角形。同理，$\Delta G{{Q}_{1}}{{R}_{1}}$ 是正三角形。设 $U$、$V$ 分别是 ${{P}_{1}}{{S}_{1}}$、${{Q}_{1}}{{R}_{1}}$ 的中点。则 $EG\leqslant EU+UV+VG=\frac{\sqrt{3}}{2}{{P}_{1}}{{S}_{1}}+{{P}_{1}}{{Q}_{1}}+\frac{\sqrt{3}}{2}{{Q}_{1}}{{R}_{1}}={{P}_{1}}{{Q}_{1}}+\sqrt{3}{{P}_{1}}{{S}_{1}}=\frac{1}{2}BD+\frac{\sqrt{3}}{2}BD$ 把上面两式相加得 $y\leqslant\frac{1+\sqrt{3}}{2}x$，即 $\frac{y}{x}\leqslant \frac{1+\sqrt{3}}{2}$ 。
联结 ${{P}_{1}}E$、${{S}_{1}}E$ 。设 $M$、$N$ 分别是 $DP$、$DS$ 的中点。则 $D{{S}_{1}}={{S}_{1}}N=DN=EM$，$D{{P}_{1}}={{P}_{1}}M=MD=EN$ 。又 $\angle {{P}_{1}}D{{S}_{1}}={{360}^{{}^\circ}}-{{60}^{{}^\circ }}-{{60}^{{}^\circ }}-\angle PDS={{240}^{{}^\circ }}-\left({{180}^{{}^\circ }}-\angle END \right)={{60}^{{}^\circ }}+\angle END=\angle EN{{S}_{1}}=\angle EM{{P}_{1}}$ 则 $\Delta D{{P}_{1}}{{S}_{1}}\cong \Delta M{{P}_{1}}E\cong \Delta NE{{S}_{1}}$，从而 $\Delta E{{P}_{1}}{{S}_{1}}$ 是正三角形。同理，$\Delta G{{Q}_{1}}{{R}_{1}}$ 是正三角形。设 $U$、$V$ 分别是 ${{P}_{1}}{{S}_{1}}$、${{Q}_{1}}{{R}_{1}}$ 的中点。则 $EG\leqslant EU+UV+VG=\frac{\sqrt{3}}{2}{{P}_{1}}{{S}_{1}}+{{P}_{1}}{{Q}_{1}}+\frac{\sqrt{3}}{2}{{Q}_{1}}{{R}_{1}}={{P}_{1}}{{Q}_{1}}+\sqrt{3}{{P}_{1}}{{S}_{1}}=\frac{1}{2}BD+\frac{\sqrt{3}}{2}BD$ 把上面两式相加得 $y\leqslant\frac{1+\sqrt{3}}{2}x$，即 $\frac{y}{x}\leqslant \frac{1+\sqrt{3}}{2}$ 。
答案
解析
备注
