如图，已知凸四边形 $ABCD$ 满足 $AB=BC$，$AD=DC$，$E$、$F$ 分别是线段 $AB$、$AD$ 上一点，满足 $B$、$E$、$F$、$D$ 四点共圆。作 $\Delta DPE$ 顺向相似于 $\Delta ADC$，作 $\Delta BQF$ 顺向相似于 $\Delta ABC$ 。求证：$A$、$P$、$Q$ 三点共线。 注：两个三角形顺向相似是指他们的对应顶点按顺时针方向或按逆时针方向排列。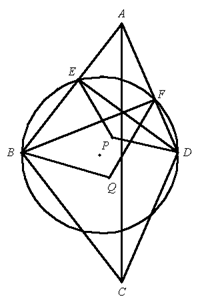
【难度】
【出处】
2008第7届CGMO试题
【标注】
【答案】
略
【解析】
如图，将 $B$、$E$、$F$、$D$ 四点所共圆的圆心记作 $O$ 。联结 $OB$、$OF$、$BD$ 。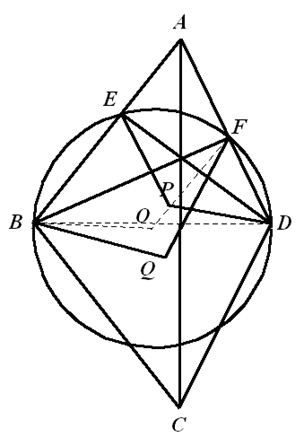
在 $\Delta BDF$ 中，$O$ 是外心，故 $\angle BOF=2\angle BDA$ 。又 $\Delta ABD\sim \Delta CBD$，则 $\angle CDA=2\angle BDA$ 。于是，$\angle BOF=\angle CDA=\angle EPD$ 。由此知 $\Delta BOF\sim\Delta EPD$（1）。另一方面，由 $B$、$E$、$F$、$D$ 四点共圆知 $\Delta ABF\sim \Delta ADE$（2）。综合（1）（2）知，四边形 $ABOF\sim ADPE$ 。由此得 $\angle BAO=\angle DAP$（3）。同理 $\angle BAO=\angle DAQ$（4）。（3）（4）表明 $A$、$P$、$Q$ 三点共线。
在 $\Delta BDF$ 中，$O$ 是外心，故 $\angle BOF=2\angle BDA$ 。又 $\Delta ABD\sim \Delta CBD$，则 $\angle CDA=2\angle BDA$ 。于是，$\angle BOF=\angle CDA=\angle EPD$ 。由此知 $\Delta BOF\sim\Delta EPD$（1）。另一方面，由 $B$、$E$、$F$、$D$ 四点共圆知 $\Delta ABF\sim \Delta ADE$（2）。综合（1）（2）知，四边形 $ABOF\sim ADPE$ 。由此得 $\angle BAO=\angle DAP$（3）。同理 $\angle BAO=\angle DAQ$（4）。（3）（4）表明 $A$、$P$、$Q$ 三点共线。
答案
解析
备注
