给定一个 $2008\times 2008$ 的棋盘，棋盘上每个小方格的颜色均不相同，在棋盘的每个小方格中填入 $C$、$G$、$M$、$O$ 这 $4$ 个字母中的一个，若棋盘中每一个 $2\times 2$ 的小棋盘中都有 $C$、$G$、$M$、$O$ 这 $4$ 个字母，则称这个棋盘为“和谐棋盘”。问有多少种不同的和谐棋盘？
【难度】
【出处】
2008第7届CGMO试题
【标注】
【答案】
24
【解析】
有 $12\times {{2}^{2008}}-24$ 种不同的和谐棋盘。 首先证明一个结论：在每个和谐棋盘中，至少出现以下情况中的某一种：（1）每一行都是某两个字母交替出现；（2）每一列都是某两个字母交替出现。 事实上，假设某一行不是交替的，则这一行必定包括三个相邻的小方格填有不同的字母。不失一般性，假设这三个字母为 $C$、$G$、$M$ 。如图，易得 ${{X}_{2}}\text{=}{{X}_{5}}\text{=}O$，且 ${{X}_{1}}\text{=}{{X}_{4}}\text{=}M$ 和 ${{X}_{3}}\text{=}{{X}_{6}}\text{=}C$ 。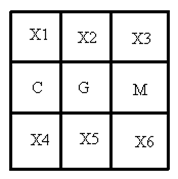
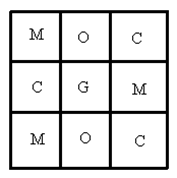同理，可以得到这三列都是两个字母交替出现。从而，易得每一列都是某两个字母交替出现。 回到原题。接下来计算和谐棋盘的个数。 如果最左边一列是两个字母（如 $C$ 和 $M$）交替出现，马上可以得到序列为奇数的列都是这两个字母交替出现，且序号为偶数的列都是另外两个字母（如 $G$ 和 $O$）交替出现。每一列的第一个字母可以是这一列所包含的两个字母的任意一个。容易验证任意这样的填写都可以得到和谐棋盘。从而，有 $C_{4}^{2}\text{=}6$ 种不同的方式选择第一列的两个字母，且有 ${{2}^{2008}}$ 种方式决定每一列的第一个字母。所以，有 $6\times{{2}^{2008}}$ 种填法使得每一列都是交替的。同样，也有 $6\times {{2}^{2008}}$ 种填法使得每一行都是交替的。 下面要做的就是从中减去计算了两次的填法—行和列都是交替的。 显然，四个不同字母的左上角的 $2\times2$ 方格中的任何排列都可以扩充到整个棋盘得到一个和谐棋盘，并且行和列都是交替的。 事实上，只要先填好前两列使得它们是交替的，再填所有的行使得它们是交替的即可。反过来，这种双交替的填法由左上角的 $2\times2$ 方格唯一决定。有 $4\text{!=}24$ 种方式在左上角的 $2\times 2$ 方格中排列四个不同的字母。所以，得到 $24$ 种不同的填法使得行和列都是交替的，由此可以得到上面结果。
同理，可以得到这三列都是两个字母交替出现。从而，易得每一列都是某两个字母交替出现。 回到原题。接下来计算和谐棋盘的个数。 如果最左边一列是两个字母（如 $C$ 和 $M$）交替出现，马上可以得到序列为奇数的列都是这两个字母交替出现，且序号为偶数的列都是另外两个字母（如 $G$ 和 $O$）交替出现。每一列的第一个字母可以是这一列所包含的两个字母的任意一个。容易验证任意这样的填写都可以得到和谐棋盘。从而，有 $C_{4}^{2}\text{=}6$ 种不同的方式选择第一列的两个字母，且有 ${{2}^{2008}}$ 种方式决定每一列的第一个字母。所以，有 $6\times{{2}^{2008}}$ 种填法使得每一列都是交替的。同样，也有 $6\times {{2}^{2008}}$ 种填法使得每一行都是交替的。 下面要做的就是从中减去计算了两次的填法—行和列都是交替的。 显然，四个不同字母的左上角的 $2\times2$ 方格中的任何排列都可以扩充到整个棋盘得到一个和谐棋盘，并且行和列都是交替的。 事实上，只要先填好前两列使得它们是交替的，再填所有的行使得它们是交替的即可。反过来，这种双交替的填法由左上角的 $2\times2$ 方格唯一决定。有 $4\text{!=}24$ 种方式在左上角的 $2\times 2$ 方格中排列四个不同的字母。所以，得到 $24$ 种不同的填法使得行和列都是交替的，由此可以得到上面结果。
答案
解析
备注
