如图，在 $\Delta ABC$ 中，$\angle BAC\text{=}{{90}^{{}^\circ }}$，点 $E$ 在 $\Delta ABC$ 的外接圆 $\Gamma $ 的弧 $BC$（不含点 $A$）内，$AE$ > $EC$ 。联结 $EC$ 并延长至点 $F$，使得 $\angle EAC=\angle CAF$，联结 $BF$ 交圆 $\Gamma $ 于点 $D$，联结 $ED$，记 $\Delta DEF$ 的外心为 $O$ 。求证：$A$、$C$、$O$ 三点共线。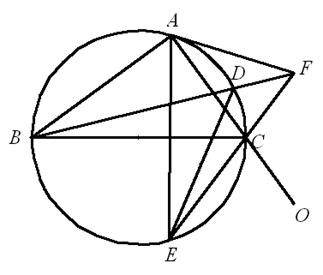
【难度】
【出处】
2009第8届CGMO试题
【标注】
【答案】
略
【解析】
用同一法。如图，设 $\Delta AEF$ 的外接圆圆 $\Gamma $ 与 $AC$ 的延长线交于点 $P$，联结 $PE$、$PF$ 。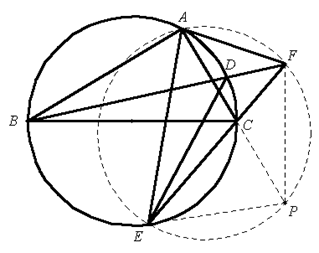
因 $\angle EAC=\angle FAC$，所以四边形 $AEPF$ 是圆内接四边形。 故 $\angle PEF=\angle PFE=\angle EAP\Rightarrow PE=PF\Rightarrow \angle EPF={{180}^{{}^\circ }}-2\angle EAP$（1）又 $E$、$D$、$A$、$B$ 四点共圆，则 $\angle BDE=\angle EAB={{90}^{{}^\circ }}-\angle EAC={{90}^{{}^\circ }}-\angle EAP$（2）由（1）（2）得 $\angle BDE=\frac{1}{2}\angle EPF$（3）以点 $P$ 为圆心、$PE$ 为半径作 $\odot P$ 。则点 $E$、$F$ 在 $\odot P$ 上。结合式（3）知，点 $D$ 也在 $\odot P$ 上。故 $P$ 为 $\Delta DEF$ 的外心。这就表明，点 $P$ 与 $O$ 重合，即 $\Delta AEF$ 的外心 $O$ 位于 $AC$ 的延长线上。
因 $\angle EAC=\angle FAC$，所以四边形 $AEPF$ 是圆内接四边形。 故 $\angle PEF=\angle PFE=\angle EAP\Rightarrow PE=PF\Rightarrow \angle EPF={{180}^{{}^\circ }}-2\angle EAP$（1）又 $E$、$D$、$A$、$B$ 四点共圆，则 $\angle BDE=\angle EAB={{90}^{{}^\circ }}-\angle EAC={{90}^{{}^\circ }}-\angle EAP$（2）由（1）（2）得 $\angle BDE=\frac{1}{2}\angle EPF$（3）以点 $P$ 为圆心、$PE$ 为半径作 $\odot P$ 。则点 $E$、$F$ 在 $\odot P$ 上。结合式（3）知，点 $D$ 也在 $\odot P$ 上。故 $P$ 为 $\Delta DEF$ 的外心。这就表明，点 $P$ 与 $O$ 重合，即 $\Delta AEF$ 的外心 $O$ 位于 $AC$ 的延长线上。
答案
解析
备注
