如图，圆 ${{\Gamma }_{1}}$、${{\Gamma }_{2}}$ 内切于点 $S$，圆 ${{\Gamma }_{2}}$ 的弦 $AB$ 与圆 ${{\Gamma }_{1}}$ 切于点 $C$，$M$ 是弧 $AB$（不含点 $S$）的中点，过点 $M$ 作 $MN\bot AB$，垂足为 $N$ 。记圆 ${{\Gamma }_{1}}$ 的半径为 $r$ 。求证：$AC\cdot CB=2r\cdot MN$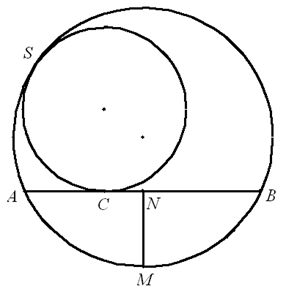
【难度】
【出处】
2009第8届CGMO试题
【标注】
【答案】
略
【解析】
证法1：如图，作出圆 ${{\Gamma }_{1}}$ 的直径 $CD$ 。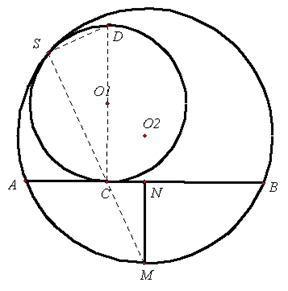
因 $S$ 是圆 ${{\Gamma }_{1}}$、${{\Gamma }_{2}}$ 的公切点，即位似中心，而 $C$、$M$ 为两圆上的位似对应点，故 $S$、$C$、$M$ 三点共线。由相交弦定理得 $AC\cdot CB=SC\cdot CM$ 。 又由 $Rt\Delta SCD\sim Rt\Delta NMC$，得 $SC\cdot CM=CD\cdot MN=2r\cdot MN$ 。 证法2：如图，记圆 ${{\Gamma}_{1}}$、${{\Gamma }_{2}}$ 的圆心分别为 ${{O}_{1}}$、${{O}_{2}}$，半径分别为 $r$、$R$ 。
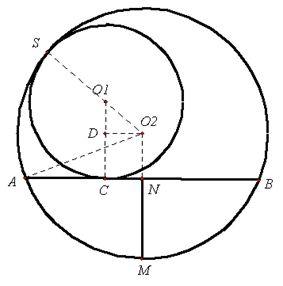由垂径定理知，$MN$ 的延长线经过 ${{O}_{2}}$，且 $N$ 是弦 $AB$ 的中点。 因圆 ${{\Gamma}_{1}}$、${{\Gamma }_{2}}$ 内切于点 $S$，所以 $S$、${{O}_{1}}$、${{O}_{2}}$ 三点共线。 又 $AB$ 与圆 ${{\Gamma}_{1}}$ 切于点 $C$，联结 ${{O}_{1}}C$，则 ${{O}_{1}}C\bot AB$ 。作 ${{O}_{1}}D\bot {{O}_{1}}C$ 于 $D$ 。 注意到 $AC\cdot CB=\left( AN-CN \right)\left( AN+CN \right)=A{{N}^{2}}-C{{N}^{2}}$（1）联结 $A{{O}_{2}}$，由勾股定理得 $A{{N}^{2}}={{R}^{2}}-{{\left(R-MN \right)}^{2}}=2R\cdot MN-M{{N}^{2}}$（2）而 $C{{N}^{2}}={{O}_{1}}O_{2}^{2}-{{O}_{1}}{{D}^{2}}={{\left(R-r \right)}^{2}}-{{\left( r+MN-R \right)}^{2}}=2\left( R-r \right)\cdot MN-M{{N}^{2}}$（3）将式（2）（3）代入式（1）得到 $AC\cdot CB=A{{N}^{2}}-C{{N}^{2}}=2\left[ R-\left( R-r \right) \right]\cdot MN=2r\cdot MN$
因 $S$ 是圆 ${{\Gamma }_{1}}$、${{\Gamma }_{2}}$ 的公切点，即位似中心，而 $C$、$M$ 为两圆上的位似对应点，故 $S$、$C$、$M$ 三点共线。由相交弦定理得 $AC\cdot CB=SC\cdot CM$ 。 又由 $Rt\Delta SCD\sim Rt\Delta NMC$，得 $SC\cdot CM=CD\cdot MN=2r\cdot MN$ 。 证法2：如图，记圆 ${{\Gamma}_{1}}$、${{\Gamma }_{2}}$ 的圆心分别为 ${{O}_{1}}$、${{O}_{2}}$，半径分别为 $r$、$R$ 。由垂径定理知，$MN$ 的延长线经过 ${{O}_{2}}$，且 $N$ 是弦 $AB$ 的中点。 因圆 ${{\Gamma}_{1}}$、${{\Gamma }_{2}}$ 内切于点 $S$，所以 $S$、${{O}_{1}}$、${{O}_{2}}$ 三点共线。 又 $AB$ 与圆 ${{\Gamma}_{1}}$ 切于点 $C$，联结 ${{O}_{1}}C$，则 ${{O}_{1}}C\bot AB$ 。作 ${{O}_{1}}D\bot {{O}_{1}}C$ 于 $D$ 。 注意到 $AC\cdot CB=\left( AN-CN \right)\left( AN+CN \right)=A{{N}^{2}}-C{{N}^{2}}$（1）联结 $A{{O}_{2}}$，由勾股定理得 $A{{N}^{2}}={{R}^{2}}-{{\left(R-MN \right)}^{2}}=2R\cdot MN-M{{N}^{2}}$（2）而 $C{{N}^{2}}={{O}_{1}}O_{2}^{2}-{{O}_{1}}{{D}^{2}}={{\left(R-r \right)}^{2}}-{{\left( r+MN-R \right)}^{2}}=2\left( R-r \right)\cdot MN-M{{N}^{2}}$（3）将式（2）（3）代入式（1）得到 $AC\cdot CB=A{{N}^{2}}-C{{N}^{2}}=2\left[ R-\left( R-r \right) \right]\cdot MN=2r\cdot MN$
答案
解析
备注
