在一个 $10\times 10$ 的方格表中有一个由 $4n$ 个 $1\times 1$ 的小方格组成的图形，它即可被 $n$ 个“
”型的图形覆盖，也可被 $n$ 个“
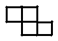”或“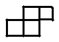
”型（可以旋转）的图形覆盖。求正整数 $n$ 的最小值。
”型的图形覆盖，也可被 $n$ 个“”或“”型（可以旋转）的图形覆盖。求正整数 $n$ 的最小值。【难度】
【出处】
2009第8届CGMO试题
【标注】
【答案】
略
【解析】
将题设的图形分别设为 $A$ 型、$B$ 型。 首先论证 $n$ 是偶数。用图1的方法将 $10\times 10$ 的方格表染色。
图1 无论 $A$ 型覆盖哪4个方格，其中黑格数必是偶数，而对于 $B$ 型则是奇数。如果 $n$ 是奇数，$n$ 个 $A$ 型所覆盖的黑方格数必是偶数；而 $n$ 个 $B$ 型所覆盖的黑方格数必是奇数，矛盾。所以，$n$ 是偶数。 如果 $n\text{=}2$，由两个 $A$ 型拼成的图形只有图2的两种情形。但是它们都不能由两个 $B$ 型拼成。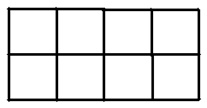
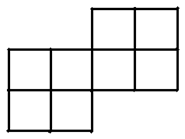图2 所以，$n\geqslant 4$ 。图3为 $n\text{=}4$ 时的拼法。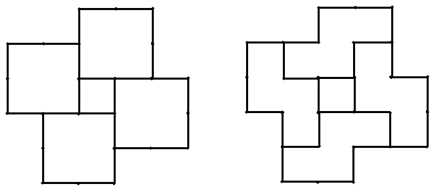
图1 无论 $A$ 型覆盖哪4个方格，其中黑格数必是偶数，而对于 $B$ 型则是奇数。如果 $n$ 是奇数，$n$ 个 $A$ 型所覆盖的黑方格数必是偶数；而 $n$ 个 $B$ 型所覆盖的黑方格数必是奇数，矛盾。所以，$n$ 是偶数。 如果 $n\text{=}2$，由两个 $A$ 型拼成的图形只有图2的两种情形。但是它们都不能由两个 $B$ 型拼成。图2 所以，$n\geqslant 4$ 。图3为 $n\text{=}4$ 时的拼法。
答案
解析
备注
